题目内容
17.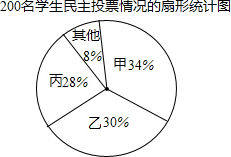 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:| 试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
分析 (1)由题意可分别求得三人的得票数,甲的得票数=200×34%,乙的得票数=200×30%,丙的得票数=200×28%;
(2)由题意可分别求得三人的得分,比较得出结论.
解答 解:(1)甲的票数是:200×34%=68(票),
乙的票数是:200×30%=60(票),
丙的票数是:200×28%=56(票);
(2)甲的平均成绩:$\frac{68×2+92×5+85×3}{2+5+3}=85.1$分,
乙的平均成绩:$\frac{60×2+90×5+95×3}{2+5+3}=85.5$分,
丙的平均成绩:$\frac{56×2+95×5+80×3}{2+5+3}=82.7$分,
∵乙的平均成绩最高,
∴应该录取乙.
点评 本题考查了扇形统计图以及加权平均数的求法.重点考查了理解统计图的能力和平均数的计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列运算正确的是( )
| A. | -a(a-b)=-a2-ab | B. | (2ab)2÷a2b=4ab | C. | 2ab•3a=6a2b | D. | (a-1)(1-a)=a2-1 |
5.当$\frac{2x-1}{xy}$=$\frac{k}{{3x}^{2}{y}^{2}}$时,k的值为( )
| A. | 3x2y2(2x-1) | B. | 3xy(2x-1) | C. | xy2(2x-1) | D. | xy(2x-1) |
2.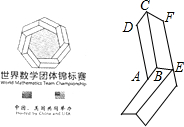 第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
 第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )
第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )| A. | 7(a+b+c-d) | B. | 7(a+b-c+d) | C. | 7(a-b+c+d) | D. | 7(b+c+d-a) |
9.某商场统计了去年1~5月A,B两种品牌冰箱的销售情况.
则这段时间内这两种品牌冰箱月销售量较稳定的是A(填“A”或“B”).
| A品牌(台) | 15 | 17 | 16 | 13 | 14 |
| B品牌(台) | 10 | 14 | 15 | 16 | 20 |
6.关于x的方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )
| A. | m≤2 | B. | m<2 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
7.在△ABC中,∠C=90°,∠A=30°,若CD是高,且CD=1,则a,b,c三边的长分别是( )
| A. | a=$\sqrt{3}$,b=2,c=$\sqrt{7}$ | B. | a=2,b=$\frac{2\sqrt{3}}{3}$,c=$\frac{4\sqrt{3}}{3}$ | C. | a=$\frac{2\sqrt{3}}{3}$,b=2,c=$\frac{4\sqrt{3}}{3}$ | D. | a=2,b=2,c=4 |