题目内容
4.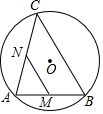 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.
如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.
分析 根据中位线定理得到MN的长最大时,BC最大,当BC最大时是直径,从而求得直径后就可以求得最大值.
解答  解:如图,∵点M,N分别是AB,AC的中点,
解:如图,∵点M,N分别是AB,AC的中点,
∴MN=$\frac{1}{2}$BC,
∴当BC取得最大值时,MN就取得最大值,当BC是直径时,BC最大,
连接BO并延长交⊙O于点C′,连接AC′,
∵BC′是⊙O的直径,
∴∠BAC′=90°.
∵∠ACB=45°,AB=5,
∴∠AC′B=45°,
∴BC′=$\frac{AB}{sin45°}$=$\frac{5}{\frac{\sqrt{2}}{2}}$=5$\sqrt{2}$,
∴MN最大=$\frac{5\sqrt{2}}{2}$.
故答案为:$\frac{5\sqrt{2}}{2}$.
点评 本题考查了三角形的中位线定理、等腰直角三角形的性质及圆周角定理,解题的关键是了解当什么时候MN的值最大,难度不大.

练习册系列答案
相关题目
12.下面调查中,适合采用普查的是( )
| A. | 调查你所在的班级同学的身高情况 | B. | 调查全国中学生心理健康现状 | ||
| C. | 调查我市食品合格情况 | D. | 调查中央电视台《少儿节目》收视率 |
13.关于x的一元一次不等式$\frac{m-2x}{3}$≤-2的解集为x≥4,则m的值为( )
| A. | 14 | B. | 7 | C. | -2 | D. | 2 |
 如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.
如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.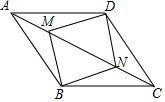 如图,点M、N在?ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.
如图,点M、N在?ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.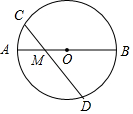 如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$.
如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1). 在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.