题目内容
9.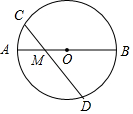 如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$.
如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$.
分析 连接OD,作OE⊥CD于E,由垂径定理得出CE=DE,证明△OEM是等腰直角三角形,由勾股定理得出OE=$\frac{\sqrt{2}}{2}$OM=$\frac{\sqrt{2}}{2}$,在Rt△ODE中,由勾股定理求出DE=$\frac{\sqrt{14}}{2}$,得出CD=2DE=$\sqrt{14}$即可.
解答 解:连接OD,作OE⊥CD于E,如图所示: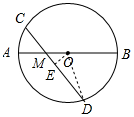
则CE=DE,
∵AB是⊙O的直径,AB=4,点M是OA的中点,
∴OD=OA=2,OM=1,
∵∠OME=∠CMA=45°,
∴△OEM是等腰直角三角形,
∴OE=$\frac{\sqrt{2}}{2}$OM=$\frac{\sqrt{2}}{2}$,
在Rt△ODE中,由勾股定理得:DE=$\sqrt{{2}^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{14}}{2}$,
∴CD=2DE=$\sqrt{14}$;
故答案为:$\sqrt{14}$.
点评 本题考查了垂径定理、勾股定理、等腰直角三角形的判定与性质;熟练掌握垂径定理,由勾股定理求出DE是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.通过估算,估计$\sqrt{19}$的值应在( )
| A. | 2~3之间 | B. | 3~4之间 | C. | 4~5之间 | D. | 5~6之间 |
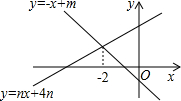 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )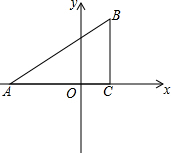 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=$\frac{3}{4}$AC
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=$\frac{3}{4}$AC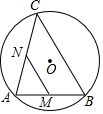 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.
如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.