题目内容
4. 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.(1)求证:DF是⊙O的切线;
(2)若$sinC=\frac{{\sqrt{3}}}{4}$,半径OA=4,求AE的长.
分析 (1)连接OD,由OB=OD得出∠B=∠ODB.根据AB=AC得出∠B=∠C.故可得出∠ODB=∠C,所以OD∥AC.由DF⊥AC,得出OD⊥DF,故可得出结论;
(2)连结BE,AD,根据圆周角定理得出∠ADB=90°,∠AEB=90°.再由AB=AC,可知∠ABC=∠C,BD=CD.在Rt△ABD 中,利用锐角三角函数的定义得出AD及BD的长,同理可得出BE的长,由勾股定理求出CE的长,进而可得出结论.
解答 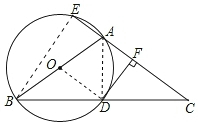 (1)证明:连接OD.
(1)证明:连接OD.
∵OB=OD,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C.
∴∠ODB=∠C.
∴OD∥AC.
∵DF⊥AC,
∴OD⊥DF.
∴DF是⊙O的切线;
(2)解:连结BE,AD.
∵AB是直径,
∴∠ADB=90°,∠AEB=90°.
∵AB=AC,
∴∠ABC=∠C,BD=CD.
在Rt△ABD 中,
∵OA=4,sinC=$\frac{\sqrt{3}}{4}$,
∴$\frac{AD}{AB}$=$\frac{AD}{8}$=$\frac{\sqrt{3}}{4}$,
∴AD=2$\sqrt{3}$,BD=2$\sqrt{13}$,
∴BC=4$\sqrt{13}$.
在Rt△BCE 中,
∵sinC=$\frac{BE}{BC}$=$\frac{\sqrt{3}}{4}$,即$\frac{BE}{4\sqrt{13}}$=$\frac{\sqrt{3}}{4}$,
∴BE=$\sqrt{39}$,
∴CE=$\sqrt{{BC}^{2}-{BE}^{2}}$=$\sqrt{{(4\sqrt{13})}^{2}-{(\sqrt{39})}^{2}}$=13,
∴AE=CE-AC=5.
点评 本题考查的是切线的判定定理,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

 已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
 如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )
如图,在?ABCD中,AC与BD交于O点,则下列结论中不一定成立的是( )| A. | AB=CD | B. | AO=CO | C. | AC=BD | D. | BO=DO |
| A. | 旋转一定会改变图形的形状和大小 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| D. | 相等的角是对顶角 |
 如图,在?ABCD中,BE平分∠ABC,∠D=80°,则∠AEB=40°.
如图,在?ABCD中,BE平分∠ABC,∠D=80°,则∠AEB=40°.