题目内容
6.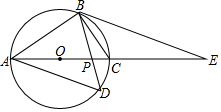 如图,四边形ABCD内接于⊙O,AC是⊙O的直径,AB=BD,BD交AC于P,过B作BE∥AD交AC和延长线于E.
如图,四边形ABCD内接于⊙O,AC是⊙O的直径,AB=BD,BD交AC于P,过B作BE∥AD交AC和延长线于E.(1)求证:BE是⊙O的切线;
(2)若AC=8,PC=1,求tan∠CBD的值.
分析 (1)连接OB并延长交AD于F,连接OD,根据全等三角形的性质得到∠ABO=∠DBO,推出BE∥AD,证得∠OBE=90°,根据切线的判定定理即可得到结论;
(2)根据已知条件得到CD∥BF,根据平行线分线段成比例定理得到CD=$\frac{4}{3}$,根据勾股定理得到AD=$\frac{4}{3}$$\sqrt{35}$,解直角三角形即可得到结论.
解答 解:(1)连接OB并延长交AD于F,连接OD,
在△ABO与△DBO中,$\left\{\begin{array}{l}{AB=BD}\\{OB=OB}\\{OA=OD}\end{array}\right.$,
∴△ABD≌△DBO,
∴∠ABO=∠DBO,
∴BF⊥AD,
∴∠BDF+∠OBD=90°,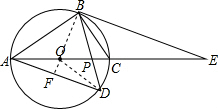
∵BE∥AD,
∴∠EBD=∠BDF,∴∠EBD+∠OBD=90°,
即∠OBE=90°,
∴BE是⊙O的切线;
(2)∵BF⊥AD,CD⊥AD,
∴CD∥BF,
∴$\frac{CD}{BO}=\frac{CP}{PO}=\frac{1}{3}$,∴CD=$\frac{4}{3}$,∴AD=$\sqrt{{8}^{2}+(\frac{4}{3})^{2}}$=$\frac{4}{3}$$\sqrt{35}$,∴tan∠CAD=$\frac{CD}{AD}$=$\frac{\sqrt{35}}{35}$,
∵∠CBD=∠CAD,
∴tan∠CBD=$\frac{\sqrt{35}}{35}$.
点评 本题考查了切线的判定,平行线的性质,平行线分线段成比例定理,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
17.如果|x+y-3|=2x+2y,那么(x+y)3的值为( )
| A. | 1 | B. | -27 | C. | 1或-27 | D. | 1或27 |
14.如图是正方形卡片A类、B类和长方形卡片C类.现有A类卡片4张,B类卡片1张,C类卡片4张,则这9张卡片能拼成的正方形的边长为( )
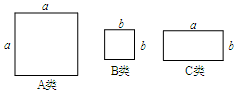

| A. | a+2b | B. | 2a+b | C. | 2a+2b | D. | a+b |
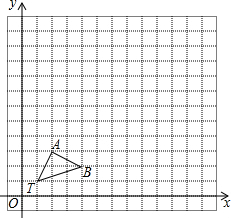 在12×12的正方形网格中,△TAB的顶点坐标为T(1,1)、A(2,3)、B(4,2)
在12×12的正方形网格中,△TAB的顶点坐标为T(1,1)、A(2,3)、B(4,2) .
. ,求锐角α.
,求锐角α. 的值.
的值.