题目内容

14．如图是正方形卡片A类、B类和长方形卡片C类．现有A类卡片4张，B类卡片1张，C类卡片4张，则这9张卡片能拼成的正方形的边长为（　　）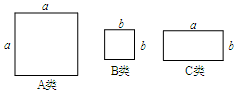
A．a+2bB．2a+bC．2a+2bD．a+b

分析 根据题意得到所求的正方形的面积等于4张正方形A类卡片、1张正方形B类卡片和4张长方形C类卡片的和，则所求正方形的面积=4a2+b2+4ab，运用完全平方公式得到所求正方形的面积=（2a+b）2，则所求正方形的边长为2a+b．

解答 解：∵所求的正方形的面积等于4张正方形A类卡片、1张正方形B类卡片和4张长方形C类卡片的和，
∴所求正方形的面积=4a2+b2+4ab=（2a+b）2，
∴所求正方形的边长为2a+b．
故选：B．

点评 本题考查了正方形的面积公式的运用以及完全平方公式的几何背景：通过几何图形面积关系证明完全平方公式．解题时注意数形结合思想的运用．

练习册系列答案
相关题目
4．如图1所示，在A，B两地之间有汽车站C，客车由A地驶往C站，货车由B地驶往A地，两车同时出发，匀速行驶．图2是客车、货车离C站的距离y1，y2（千米）与行驶时间x（小时）之间的函数图象．
（1）①A，B两地的距离为440千米；②货车的速度是40千米/小时；
（2）求点E的坐标，并说明点E的实际意义．
5．下列四个关系式中，y是x的反比例函数的是（　　）
A．y=4xB．y=$\frac{1}{3x}$C．y=$\frac{1}{{x}^{2}}$D．y=$\frac{1}{x+1}$
2．解下列不等式（组），并把解集在数轴上表示出来：
（1）$\left\{\begin{array}{l}{5x-3＜41}\\{4（x-1）+3≥2x}\end{array}\right.$
（2）$\frac{3y-1}{2}$＜$\frac{10y+5}{6}$-1．
9．已知P=m2-2m，Q=2m-4，则P，Q的大小关系为（　　）
A．P≥QB．P＞QC．P≤QD．P＜Q
19．两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S1；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S2．
（1）用含a、b的代数式分别表示S1、S2；
（2）若a+b=10，ab=23，求S1+S2的值；
（3）当S1+S2=29时，求出图3中阴影部分的面积S3．
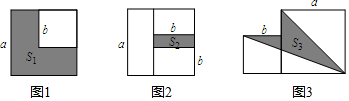
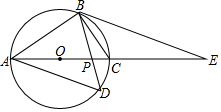6．如图，四边形ABCD内接于⊙O，AC是⊙O的直径，AB=BD，BD交AC于P，过B作BE∥AD交AC和延长线于E．
（1）求证：BE是⊙O的切线；
（2）若AC=8，PC=1，求tan∠CBD的值．

若关于的方程的解为，则＝__________；

如图，在Rt△ABC中，∠C=90°，∠ABC的平分线交AC于点D，点O是AB上一点，⊙O过B、D两点，且分别交AB、BC于点E、F．

(1) 求证：AC是⊙O的切线；

(2) 已知AB=10，BC=6，求⊙O的半径r．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网