题目内容
1.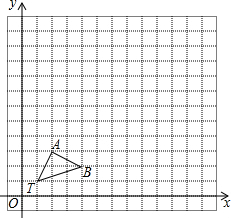 在12×12的正方形网格中,△TAB的顶点坐标为T(1,1)、A(2,3)、B(4,2)
在12×12的正方形网格中,△TAB的顶点坐标为T(1,1)、A(2,3)、B(4,2)(1)以原点(0,0)为位似中心,相似比2:1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标(2a,2b).
分析 (1)根据题目的叙述,正确地作出图形,然后确定各点的坐标即可;
(2)根据(1)中变换的规律,即可写出变化后点C的对应点C′的坐标.
解答  解:(1)如图所示:△T′A′B′即为所求,A′(4,6),B′(8,4);
解:(1)如图所示:△T′A′B′即为所求,A′(4,6),B′(8,4);
(2)变化后点C的对应点C′的坐标为:C′(2a,2b).
故答案为:(2a,2b).
点评 本题考查位似变换作图的问题,正确理解位似变换的定义,会进行位似变换的作图是解题的关键.

练习册系列答案
相关题目
9.已知P=m2-2m,Q=2m-4,则P,Q的大小关系为( )
| A. | P≥Q | B. | P>Q | C. | P≤Q | D. | P<Q |
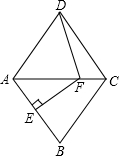 如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,且∠CDF=27°,则∠DAF等于51度.
如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,且∠CDF=27°,则∠DAF等于51度.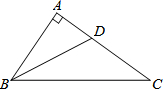 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AB=6,BC=10,则AD为3.
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AB=6,BC=10,则AD为3. 如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中:
如图为某地区今年4月的均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中: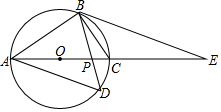 如图,四边形ABCD内接于⊙O,AC是⊙O的直径,AB=BD,BD交AC于P,过B作BE∥AD交AC和延长线于E.
如图,四边形ABCD内接于⊙O,AC是⊙O的直径,AB=BD,BD交AC于P,过B作BE∥AD交AC和延长线于E. ,求BF的长.
,求BF的长.

 B.
B.  C.
C.  D.
D. 
 =____.
=____.