题目内容
3.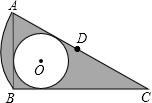 如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.
分析 连接BD,解直角三角形得到AC=2,BC=$\sqrt{3}$,由点D是AC的中点,得到AD=BD=AB=CD,求得∠ADB=60°,然后根据图形的面积公式即可得到结论.
解答 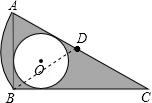 解:连接BD,在Rt△ABC中,AB=1,∠ACB=30°,
解:连接BD,在Rt△ABC中,AB=1,∠ACB=30°,
∴AC=2,BC=$\sqrt{3}$,
∵点D是AC的中点,
∴AD=BD=AB=CD,
∴∠ADB=60°,
∴⊙O的半径=$\frac{1+\sqrt{3}-2}{2}$=$\frac{\sqrt{3}-1}{2}$,
∴S阴影=S扇形ABD-S△ABD+S△ABC-S圆O=$\frac{60•π×{1}^{2}}{360}$-$\frac{1}{2}$×$\frac{1}{2}$×1×$\sqrt{3}$+$\frac{1}{2}$×1×$\sqrt{3}$-($\frac{\sqrt{3}-1}{2}$)2π=$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.
点评 本题考查了扇形的面积,解直角三角形,三角形的内切圆与内心,熟练掌握扇形的面积公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.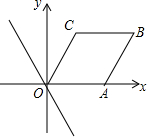 如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是( )
如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是( )
 如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是( )
如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是( )| A. | 0<m<8 | B. | 0<m<4 | C. | 2<m<8 | D. | 4≤m≤8 |
11. 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为5个;进球数的中位数为5个,众数为4个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).
 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定时定点投篮人均进球数为5个;进球数的中位数为5个,众数为4个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).


 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示. 如图是一个由两个小正方体和一个圆锥组成的几何体,它的左视图是( )
如图是一个由两个小正方体和一个圆锥组成的几何体,它的左视图是( )


