题目内容
14.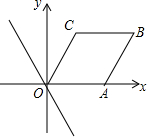 如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是( )
如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是( )| A. | 0<m<8 | B. | 0<m<4 | C. | 2<m<8 | D. | 4≤m≤8 |
分析 设平移后的直线解析式为y=-2x+b.根据平行四边形的性质结合点O、A、C的坐标即可求出点B的坐标,再由平移后的直线与边BC有交点,可得出关于b的一元一次不等式组,解不等式组即可得出结论.
解答 解:设平移后的直线解析式为y=-2x+b.
∵四边形OABC为平行四边形,且点A(2,0),O(0,0),C(1,2),
∴点B(3,2).
∵平移后的直线与边BC有交点,
∴$\left\{\begin{array}{l}{-2+b≥2}\\{-6+b≤2}\end{array}\right.$,
解得:4≤b≤8.
故选D.
点评 本题考查了平行四边形的性质、平移的性质以及两条直线相交的问题,解题的关键是找出关于b的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,将线段端点坐标带入直线中得出关于b的一元一次不等式组是关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
12.在一次体育达标测试中,小明所在小组的六位同学的立定跳远成绩如下(单位:m):2.00,2.11,2.21,2.15,2.20,2.17,那么这组数据的中位数是( )
| A. | 2.16 | B. | 2.15 | C. | 2.14 | D. | 2.13 |
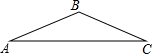 如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )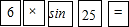



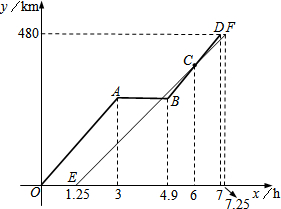 “十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.
“十•一”长假,小王与小叶相约分别驾车从南京出发,沿同一路线驶往距南京480km的甲地旅游.小王由于有事临时耽搁,比小叶迟出发1.25小时.而小叶的汽车中途发生故障,等排除故障后,立即加速赶往甲地.若从小叶出发开始计时,图中的折线O-A-B-D、线段EF分别表示小叶、小王两人与南京的距离y1(km)、y2(km)与时间x(h)之间的函数关系.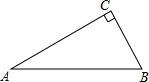 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.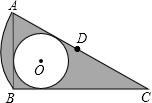 如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,AB=1,∠ACB=30°,点D是AC的中点,⊙O是△ABC的内切圆,以点D为圆心,以AD的长为半径作$\widehat{AB}$,则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$.