题目内容
18．
某种商品每天的销售利润y（元）与销售单价x（元）之间满足关系：y=ax2+bx-75，其图象如图所示．（1）求a，b的值．
（2）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？
（3）销售单价在什么范围时，该种商品每天的销售利润不低于21元？
分析 （1）利用待定系数法求二次函数解析式得出即可；
（2）利用配方法求出二次函数最值即可；
（3）根据题意令y=21，解方程可得x的值，结合图象可知x的范围．
解答 解：（1）y=ax2+bx-75图象过点（5，0）、（7，16），
∴$\left\{\begin{array}{l}{25a+5b-75=0}\\{49a+7b-75=16}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-1}\\{b=20}\end{array}\right.$．
（2）∵y=-x2+20x-75=-（x-10）2+25，
∴当x=10时，y最大=25．
答：销售单价为10元时，该种商品每天的销售利润最大，最大利润为25元；
（3）根据题意，当y=21时，得：-x2+20x-75=21，
解得：x1=8，x2=12，
即销售单价8≤x≤12时，该种商品每天的销售利润不低于21元．
点评 此题主要考查了二次函数的应用以及待定系数法求二次函数解析式等知识，正确利用二次函数图象是解题关键．
练习册系列答案
学业测评一课一测系列答案
相关题目
16．使$\sqrt{3x-1}$有意义的x的取值范围是（ ）
| A． | x＞-$\frac{1}{3}$ | B． | x＞$\frac{1}{3}$ | C． | x≥$\frac{1}{3}$ | D． | x≥-$\frac{1}{3}$ |
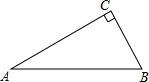如图，△ABC中，∠C=90°，∠A=30°．
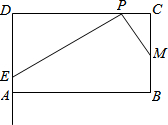如图，在矩形ABCD中，AB=m，BC=4，点M为边BC的中点，点P为边CD上的动点（点P异于C，D两点）．连接PM，过点P作PM的垂线与射线DA相交于点E（如图）．
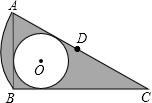如图，在Rt△ABC中，AB=1，∠ACB=30°，点D是AC的中点，⊙O是△ABC的内切圆，以点D为圆心，以AD的长为半径作$\widehat{AB}$，则图中阴影部分的面积是$\frac{3\sqrt{3}-5}{6}$π+$\frac{\sqrt{3}}{4}$．
