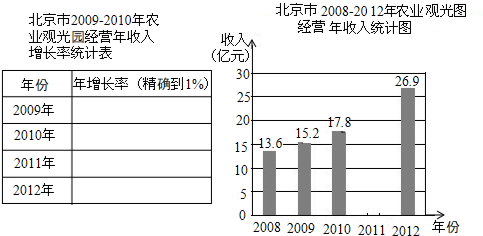
题目内容
5.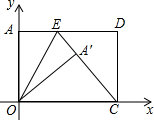 如图,在矩形AOCD中,A(0,15),E在AD上,AE=9,连接CE、OE,将矩形AOCD沿OE折叠,点A恰好落在CE上A′处,求A′的坐标.
如图,在矩形AOCD中,A(0,15),E在AD上,AE=9,连接CE、OE,将矩形AOCD沿OE折叠,点A恰好落在CE上A′处,求A′的坐标.
分析 由题意易证得△A′OC≌△DCE(AAS),OC=AD,A′O=AO=CD=15cm,设A′C=xcm,在Rt△A′OC中,由勾股定理可得OC2=A′O2+A′C2,即可得方程,解方程得出A′C,作A′F⊥OC于F,由△A′OC的面积求出A′F,再由勾股定理求出OF,即可得出点A′的坐标.
解答 解:∵四边形ABCD是矩形,
∴AO=CD=15cm,∠A=∠D=90°,AD∥OC,AD=OC,
∴∠DEC=∠A′CO,
由折叠的性质,得:A′O=AO=15cm,∠OA′E=∠A=90°,
∴A′O=CD,∠OA′C=∠D=90°,
在△A′OC和△DCE中,$\left\{\begin{array}{l}{∠OA′C=∠D}&{\;}\\{∠A′CO=∠DEC}&{\;}\\{A′O=CD}&{\;}\end{array}\right.$,
∴△A′OC≌△DCE(AAS),
∴A′C=DE,
设A′C=xcm,则OC=AD=DE+AE=x+9(cm),
在Rt△A′OC中,OC2=A′O2+A′C2,
即(x+9)2=x2+152,
解得:x=8,
∴A′C=8cm,OC=8+9=17,
作A′F⊥OC于F,如图所示: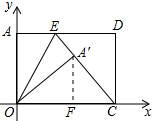
∵Rt△A′OC的面积=$\frac{1}{2}$OC•A′F=$\frac{1}{2}$OA′•A′C,
∴A′F=$\frac{15×8}{17}$=$\frac{120}{17}$,
∴OF=$\sqrt{1{5}^{2}-(\frac{120}{17})^{2}}$=$\frac{225}{17}$,
∴点A′的坐标为($\frac{225}{17}$,$\frac{120}{17}$).
点评 此题考查了矩形的性质、全等三角形的判定与性质、勾股定理以及折叠的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用,注意掌握折叠前后图形的对应关系.

| A. | 2 | B. | -8 | C. | 2或-8 | D. | 2或+8 |
| A. | 10 | B. | 4 | C. | 10或4 | D. | -10或-4 |
 如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.
如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB. 平行四边形ABCD,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内点E处.
平行四边形ABCD,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内点E处.