题目内容
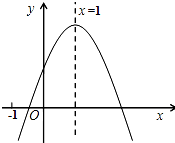 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b),(m≠1的实数)
其中正确的结论的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:用二次函数图象的开口方向,对称轴,与x、y轴的交点,以及特殊的x=1、-1、2的特殊值,进行判定即可.
解答:解:①如图,抛物线开口方向向下,则a<0.
对称轴为x=-
=1,则b=-2a>0,
抛物线与y轴交点(0,c)的纵坐标c>0,
所以,abc<0.
故①正确;
②当x=-1时,y=a-b+c<0,所以b>a+c.
故②错误;
③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0.
故③正确;
④因为a=-
b,又a-b+c<0,所以2c<3b.
故④正确;
⑤当x=1时,y的值最大.此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c>am2+bm+c,
故a+b>am2+bm,即a+b>m(am+b),故⑤错误.
综上所述,①③④正确.
故选:C.
对称轴为x=-
| b |
| 2a |
抛物线与y轴交点(0,c)的纵坐标c>0,
所以,abc<0.
故①正确;
②当x=-1时,y=a-b+c<0,所以b>a+c.
故②错误;
③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0.
故③正确;
④因为a=-
| 1 |
| 2 |
故④正确;
⑤当x=1时,y的值最大.此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c>am2+bm+c,
故a+b>am2+bm,即a+b>m(am+b),故⑤错误.
综上所述,①③④正确.
故选:C.
点评:主要考查二次函数图象与二次函数系数之间的关系,注意抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点以及一些特殊的函数值.

练习册系列答案
相关题目
 把形如△ABC的纸片按如图所示的方式折叠,当点A落在四边形BCDE内部时,下列∠A与∠1+∠2间的数量关系始终成立的是( )
把形如△ABC的纸片按如图所示的方式折叠,当点A落在四边形BCDE内部时,下列∠A与∠1+∠2间的数量关系始终成立的是( )| A、∠A=∠1+∠2 |
| B、2∠A=∠1+∠2 |
| C、3∠A=2∠1+∠2 |
| D、3∠A=2(∠1+∠2) |
如果不等式(a+1)x<a+1的解集为x>1,那么a的取值范围是( )
| A、a<1 | B、a<-1 |
| C、a>1 | D、a>-1 |
下列根式2
,
,
,
,
中,最简二次根式的个数是( )
| xy |
| 8 |
| x2-y2 |
|
| x2+4 |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列关于直线y=-x+1的结论中,正确的是( )
| A、图象必经过点(-1,1) |
| B、图象经过一、二、三象限 |
| C、当x>1时,y<0 |
| D、y随x的增大而增大 |
 如图,在四边形ADBC中,连接AB,已知∠CAB=∠DAB,∠ACB=∠ADB,求证:BC=BD.
如图,在四边形ADBC中,连接AB,已知∠CAB=∠DAB,∠ACB=∠ADB,求证:BC=BD.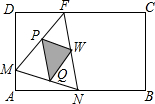 如图,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动,当动点N运动到点A时,M、N两点同时停止运动.连结FM、MN、FN,当F、N、M不在同一条直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题:
如图,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动,当动点N运动到点A时,M、N两点同时停止运动.连结FM、MN、FN,当F、N、M不在同一条直线时,可得△FMN,过△FMN三边的中点作△PQW.设动点M、N的速度都是1个单位/秒,M、N运动的时间为x秒.试解答下列问题: