题目内容
 把形如△ABC的纸片按如图所示的方式折叠,当点A落在四边形BCDE内部时,下列∠A与∠1+∠2间的数量关系始终成立的是( )
把形如△ABC的纸片按如图所示的方式折叠,当点A落在四边形BCDE内部时,下列∠A与∠1+∠2间的数量关系始终成立的是( )| A、∠A=∠1+∠2 |
| B、2∠A=∠1+∠2 |
| C、3∠A=2∠1+∠2 |
| D、3∠A=2(∠1+∠2) |
考点:三角形内角和定理,翻折变换(折叠问题)
专题:
分析:可连接AA′,分别在△AEA′、△ADA′中,利用三角形的外角性质表示出∠1、∠2;两者相加联立折叠的性质即可得到所求的结论.
解答:解:连接AA′.
则△A′ED即为折叠前的三角形,
由折叠的性质知:∠DAE=∠DA′E.
由三角形的外角性质知:
∠1=∠EAA′+∠EA′A,∠2=∠DAA′+∠DA′A;
则∠1+∠2=∠DAE+∠DA′E=2∠DAE,
即∠1+∠2=2∠A.
故选B.

则△A′ED即为折叠前的三角形,
由折叠的性质知:∠DAE=∠DA′E.
由三角形的外角性质知:
∠1=∠EAA′+∠EA′A,∠2=∠DAA′+∠DA′A;
则∠1+∠2=∠DAE+∠DA′E=2∠DAE,
即∠1+∠2=2∠A.
故选B.
点评:此题主要考查的是三角形的外角性质和图形的翻折变换,理清图中角与角的关系是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
如果方程组
的解为
,那么被“★”“■”遮住的两个数分别是( )
|
|
| A、10,4 | B、4,10 |
| C、3,10 | D、10,3 |
 如图,在平面直角坐标系中,?OABC的顶点A在x轴上,顶点B的坐标为(6,4),若直线I经过点(1,0)和?OABC对角线的交点,则直线I的函数解析式是( )
如图,在平面直角坐标系中,?OABC的顶点A在x轴上,顶点B的坐标为(6,4),若直线I经过点(1,0)和?OABC对角线的交点,则直线I的函数解析式是( )| A、y=x+1 | ||
B、y=
| ||
| C、y=3x-3 | ||
| D、y=x-1 |
用ABC分别表示学校、小明家、小红家,已知学校在小明家的南偏东25°,小红家在小明家正东,小红家在学校北偏东35°,则△ABC是( )是三角形.
| A、直角 | B、锐角 |
| C、钝角 | D、无法判断 |
 图中两直线L1、L2的交点坐标可以看作方程组( )的解.
图中两直线L1、L2的交点坐标可以看作方程组( )的解.A、
| |||||
B、
| |||||
C、
| |||||
D、
|
在平面直角坐标系中,下列各点在第三象限的是( )
| A、(1,2) |
| B、(1,-2) |
| C、(-1,2) |
| D、(-1,-2) |
若点A(2,n)在x轴上,则点B(n+2,n-5)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
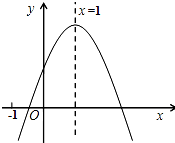 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论: