题目内容
14.下列分式是最简分式的是( )| A. | $\frac{x-1}{{x}^{2}-x}$ | B. | $\frac{x-1}{x+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{a}^{2}bc}{ab}$ |
分析 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:A、原式=$\frac{x-1}{x(x-1)}$,分子、分母中含有公因式(x-1),则它不是最简分式,故本选项错误;
B、它的分子、分母都不能再分解,且不能约分,是最简分式,故本选项正确;
C、原式=$\frac{x-1}{(x-1)(x+1)}$,分子、分母中含有公因式(x-1),则它不是最简分式,故本选项错误;
D、它的分子、分母中含有公因式ab,则它不是最简分式,故本选项错误;
故选:B.
点评 本题考查了最简分式.分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.

练习册系列答案
相关题目
9.计算(-6)×(-1)的结果等于( )
| A. | 1 | B. | -1 | C. | 6 | D. | -6 |
4.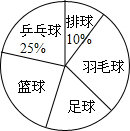 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
解答下列问题:
(1)a=30,b=24;
(2)试估计上述500名学生中最喜欢羽毛球运动的人数;
(3)该学校将组织趣味运动会,九(1)班决定从3名喜欢乒乓球、1名喜欢羽毛球,1名喜欢篮球的5名学生中随机抽取2人作为班级代表参加活动,那么被抽到的2名同学都是喜欢乒乓球的概率是多少?请用树状图或列表法说明理由.
 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的500名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:| 球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
| 人数 | a | 12 | 36 | 18 | b |
(1)a=30,b=24;
(2)试估计上述500名学生中最喜欢羽毛球运动的人数;
(3)该学校将组织趣味运动会,九(1)班决定从3名喜欢乒乓球、1名喜欢羽毛球,1名喜欢篮球的5名学生中随机抽取2人作为班级代表参加活动,那么被抽到的2名同学都是喜欢乒乓球的概率是多少?请用树状图或列表法说明理由.
 如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.
如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.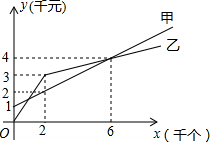 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,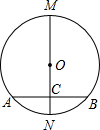 如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论: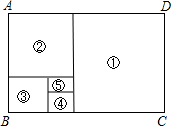 如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④
如图,在“黄金矩形”ABCD(即$\frac{宽AB}{长BC}$≈0.618)中,依次画正方形①、②、③、④