题目内容
16.当自变量x的值满足x>$\frac{1}{2}$时,直线y=-2x+1上的点在x轴的下方.分析 直线y=-2x+1上的点在x轴下方时,应有-2x+1<0,求解不等式即可.
解答 解:直线y=-2x+1上的点在x轴下方.则y<0,即-2x+1<0,
解得:x>$\frac{1}{2}$,即当自变量x的值满足x>$\frac{1}{2}$时,直线y=-2x+1上的点在x轴下方.
故答案为:x>$\frac{1}{2}$.
点评 本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
相关题目
8. 如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )
如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )
 如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )
如图,在△ABC中,AB=8,点D、E分别是AB、AC的中点,BF平分∠ABC交DE于F,则DF的长是( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 4 |
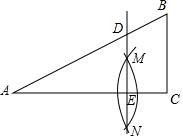 如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.
如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.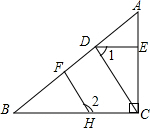 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补.求证:HF⊥AB.
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补.求证:HF⊥AB.