题目内容
7.(1)(π-2013)0+$\sqrt{12}$+|$\sqrt{3}$-2|+$\root{3}{-8}$(2)解方程组$\left\{\begin{array}{l}2(x+1)-y=6\\ \frac{x}{3}=y-1\end{array}$.
分析 (1)原式利用零指数幂,二次根式性质,以及绝对值的代数意义计算即可得到结果;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)原式=1+2$\sqrt{3}$+2-$\sqrt{3}$-2=$\sqrt{3}$+1;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-y=4①}\\{x=3y-3②}\end{array}\right.$,
把②代入①得:6y-6-y=4,
解得:y=2,
把y=2代入②得:x=3,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
2.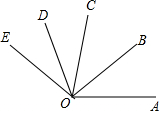 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )
 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )| A. | 50° | B. | 62° | C. | 69° | D. | 76° |
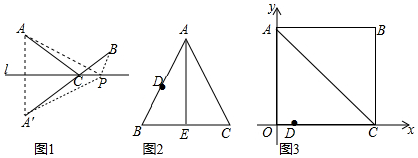
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.