题目内容
12. 如图,菱形ABCD的边长为5,以菱形ABCD的对称中心为原点O,平行于AD的直线为x轴建立平面直角坐标系,已知A(-1,2),点D在双曲线y=$\frac{k}{x}$上.
如图,菱形ABCD的边长为5,以菱形ABCD的对称中心为原点O,平行于AD的直线为x轴建立平面直角坐标系,已知A(-1,2),点D在双曲线y=$\frac{k}{x}$上.(1)写出点B、D的坐标,并求双曲线的解析式.
(2)判断点B是否在双曲线上,并说明理由.
分析 (1)直接利用菱形的性质结合A点坐标得出B,D点坐标;
(2)利用反比例函数图象上点的坐标性质得出答案.
解答 解:(1)由题意可得:B(-4,-2),D(4,2)
把D代入y=$\frac{k}{x}$得:
$2=\frac{k}{4}$,
解得:k=8
反比例函数解析式为:$y=\frac{8}{x}$;
(2)把x=-4代入解析式得:
$y=\frac{8}{-4}=-2$,
所以B(-4,-2)在双曲线上.
点评 此题主要考查了菱形的性质以及反比例函数图象上点的坐标性质,正确得出B,D点坐标是解题关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
20.下列各式中代数式的个数有( )
3x-1,a=4,S=100t+5,5xy-3,4mn,2-b>6,-2,7x2+8x-1.
3x-1,a=4,S=100t+5,5xy-3,4mn,2-b>6,-2,7x2+8x-1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )| A. | m=k | B. | m=h | C. | k>n | D. | h<0,n>0 |
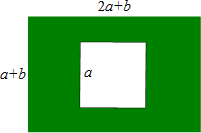 学校有一块长为2a+b米,宽为a+b米的长方形地块,学校计划将阴影部分进行绿化,并在中间修建一座正方形的凉亭,
学校有一块长为2a+b米,宽为a+b米的长方形地块,学校计划将阴影部分进行绿化,并在中间修建一座正方形的凉亭,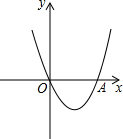 如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.
如图,已知抛物线的顶点在第四象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.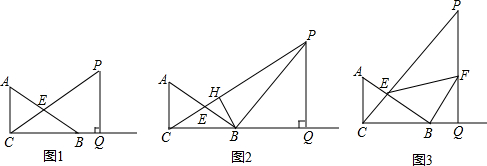
 如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.
如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.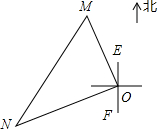 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( )
一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( ) 如图.∠1+∠2+∠3+∠4+∠5+∠6的值为720°(分割成三角形).
如图.∠1+∠2+∠3+∠4+∠5+∠6的值为720°(分割成三角形).