题目内容
已知抛物线y=-x2+2(m+1)x+m+3与x轴交于A、B两点,且OA=2OB,求二次函数的解析式.
考点:抛物线与x轴的交点
专题:计算题
分析:分类讨论:当A(-2a,0),B(a,0),根据根与系数的关系得到-2a+a=2(m+1),-2a•a=-(m+3),消去a得到m的方程2•4(m+1)2=m+3,解得m=
(舍去正号);当A(2a,0),B(-a,0)时,同样可解得m=
(舍去负号);当A(-2a,0),B(-a,0)或当A(2a,0),B(a,0)时,用同样的方法得到关于m的方程无解,然后写出满足条件的两个二次函数解析式.
-15±
| ||
| 16 |
-15±
| ||
| 16 |
解答:解:当A(-2a,0),B(a,0),则-2a+a=2(m+1),-2a•a=-(m+3),则a=-2(m+1),
∴2•4(m+1)2=m+3,解得m=
(由于m+1<0,正号舍去),
∴此时抛物线的解析式为y=-x2+
x+
;
当A(2a,0),B(-a,0),则2a-a=2(m+1),2a•(-a)=-(m+3),则a=2(m+1),
∴2•4(m+1)2=m+3,解得m=
(由于m+1>0,负号舍去),
∴此时抛物线的解析式为y=-x2+
x+
;
当A(-2a,0),B(-a,0),则-2a-a=2(m+1),2a•a=-(m+3),则a=-
(m+1),
∴2•
(m+1)2=-m-3,
整理得8m2+25m+35=0,此方程无解;
当A(2a,0),B(a,0),则2a+a=2(m+1),2a•a=-(m+3),则a=
(m+1),
∴2•
(m+1)2=-m-3,
整理得8m2+25m+35=0,此方程无解,
综上所述,二次函数的解析式为y=-x2+
x+
或y=-x2+
x+
.
∴2•4(m+1)2=m+3,解得m=
-15±
| ||
| 16 |
∴此时抛物线的解析式为y=-x2+
1-
| ||
| 8 |
33-
| ||
| 16 |
当A(2a,0),B(-a,0),则2a-a=2(m+1),2a•(-a)=-(m+3),则a=2(m+1),
∴2•4(m+1)2=m+3,解得m=
-15±
| ||
| 16 |
∴此时抛物线的解析式为y=-x2+
1+
| ||
| 8 |
33+
| ||
| 16 |
当A(-2a,0),B(-a,0),则-2a-a=2(m+1),2a•a=-(m+3),则a=-
| 2 |
| 3 |
∴2•
| 4 |
| 9 |
整理得8m2+25m+35=0,此方程无解;
当A(2a,0),B(a,0),则2a+a=2(m+1),2a•a=-(m+3),则a=
| 2 |
| 3 |
∴2•
| 4 |
| 9 |
整理得8m2+25m+35=0,此方程无解,
综上所述,二次函数的解析式为y=-x2+
1+
| ||
| 8 |
33+
| ||
| 16 |
1-
| ||
| 8 |
33-
| ||
| 16 |
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
计算:
(1)(-7)+(+10)+(-1)+(-2)
(2)-22×7-(-3)×6-5÷(-
)
(3)4x2y-8xy2+7-4x2y+10xy2-4
(4)3(2x2-xy)-4(x2-xy-6)
(1)(-7)+(+10)+(-1)+(-2)
(2)-22×7-(-3)×6-5÷(-
| 1 |
| 5 |
(3)4x2y-8xy2+7-4x2y+10xy2-4
(4)3(2x2-xy)-4(x2-xy-6)
下列说法中,正确的有( )
(1)π的相反数是-3.14;(2)-0.5的相反数是
;(3)-(-3)的相反数是3;(4)互为相反数的两个数到原点的距离相等;(5)正数和负数互为相反数;(6)相反数等于它本身的数是0.
(1)π的相反数是-3.14;(2)-0.5的相反数是
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
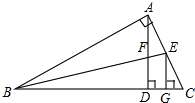 如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是( )
如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是( )| A、∠C=∠ABC |
| B、BA=BG |
| C、AE=CE |
| D、AF=FD |
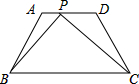 如图,在梯形ABCD中,AD∥BC,AB=CD=2,AD=5,在AD边上是否存在一点P,使得△ABP与△DPC相似?若存在,求出线段AP的长;若不存在,请说明理由.
如图,在梯形ABCD中,AD∥BC,AB=CD=2,AD=5,在AD边上是否存在一点P,使得△ABP与△DPC相似?若存在,求出线段AP的长;若不存在,请说明理由.