题目内容
19. 如图,△ABC≌△DEF,线段AD=5,DE=3,则BD=2.
如图,△ABC≌△DEF,线段AD=5,DE=3,则BD=2.
分析 根据全等三角形的性质得出AB=DE=3,即可得出答案.
解答 解:∵△ABC≌△DEF,DE=3,
∴AB=DE=3,
∵线段AD=5,
∴BD=AD-AB=5-3=2,
故答案为:2.
点评 本题考查了全等三角形的性质的应用,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等,对应边相等.

练习册系列答案
相关题目
9.下列几何体中截面不是三角形的是( )
| A. | 圆柱 | B. | 圆锥 | C. | 正方体 | D. | 正六棱柱 |
14.下面四个实数中,是无理数的是( )
| A. | 0 | B. | -$\sqrt{2}$ | C. | 3.1415 | D. | $\frac{3}{7}$ |
11.下列说法正确的是( )
| A. | 三角形三条高的交点都在三角形内 | |
| B. | 三角形的角平分线是射线 | |
| C. | 三角形三边的垂直平分线不一定交于一点 | |
| D. | 三角形三条中线的交点在三角形内 |
8.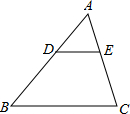 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )
 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,S△ADE:S△ABC=9:49,则EC的长是( )| A. | 4.5 | B. | 8 | C. | 10.5 | D. | 14 |