题目内容
17. 如图,扇形AOB的半径为1,∠AOB=90°,点C在线段OB上移动(不包括端点O、B),以AC为直径作半圆,弧AB与半圆AC围成的阴影部分面积为S1,弧AB与半圆AC及线段BC围成的阴影部分面积为S2,记S=S1+S2.则S的取值范围是0.3925<S<0.5.
如图,扇形AOB的半径为1,∠AOB=90°,点C在线段OB上移动(不包括端点O、B),以AC为直径作半圆,弧AB与半圆AC围成的阴影部分面积为S1,弧AB与半圆AC及线段BC围成的阴影部分面积为S2,记S=S1+S2.则S的取值范围是0.3925<S<0.5.
分析 根据题意,S1的范围是由0逐渐增大到点C与点B重合时的面积,即 S半圆AC-(S扇-S△AOB),S2的范围是由S扇-S半圆AO到0,S的范围即S1+S2的取值范围,据此解答即可.
解答 解:S1的范围是由0逐渐增大到点C与点B重合时的面积,
当点C与点B重合时,
$AC=\sqrt{{AO}^{2}{+BO}^{2}}$
=$\sqrt{{1}^{2}{+1}^{2}}$
=$\sqrt{2}$
∴S半圆AC-(S扇-S△AOB)
=$\frac{1}{2}×$3.14${×(\frac{AC}{2})}^{2}$-($\frac{1}{4}×3.14{×1}^{2}$-$\frac{1}{2}×1×1$)
=1.57${×(\frac{\sqrt{2}}{2})}^{2}$-(0.785-0.5)
=0.785-0.285
=0.5
S2的范围是由S扇-S半圆AO到0,
S扇-S半圆AO
=$\frac{1}{4}×3.14{×1}^{2}$-$\frac{1}{2}×3.14{×(\frac{1}{2})}^{2}$
=0.785-0.3925
=0.3925
∵S=S1+S2,
∴S的取值范围是:
0.3925<S<0.5.
故答案为:0.3925<S<0.5.
点评 (1)此题主要考查了扇形面积的计算,要熟练掌握,解答此题的关键是要判断出:①S1的范围是由0逐渐增大到点C与点B重合时的面积;②S2的范围是由S扇-S半圆AO到0.
(2)此题还考查了三角形的面积的求法,要熟练掌握三角形的面积公式.

练习册系列答案
相关题目
12.在平面直角坐标系中,各点的坐标分别为A1(1、3)、A2(2、5)、A3(3、7)、A4(4、9)、A5(5、11)、A6(6、13)…用你发现的规律确定A2014的坐标(2014,4029).
9.统计得到一组数据,其中最大值是132,最小值是50,取组距为10,可以分成( )
| A. | 10组 | B. | 9组 | C. | 8组 | D. | 7组 |
7.为了解本班学生每天零花钱使用情况,张明随机调查了15名同学,结果如下表:
关于这15名同学每天使用的零花钱,下列说法错误的是( )
| 每天使用零花钱(单位:元) | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A. | 众数是3元 | B. | 平均数是2.5元 | C. | 极差是5元 | D. | 中位数是3元 |
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2015=22014.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2015=22014. 已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.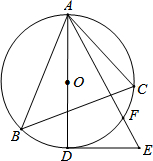 如图,已知△ABC是⊙O的圆内接三角形,AD为⊙O的直径,DE为⊙O的切线,AE交⊙O于点F,∠C=∠E.
如图,已知△ABC是⊙O的圆内接三角形,AD为⊙O的直径,DE为⊙O的切线,AE交⊙O于点F,∠C=∠E.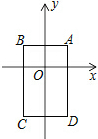 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).