题目内容
5.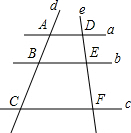 如图,直线a,b,c被直线d,e所截,a∥b∥c,$\frac{DE}{DF}$=$\frac{3}{5}$.若BC=4,则AC的长度为10.
如图,直线a,b,c被直线d,e所截,a∥b∥c,$\frac{DE}{DF}$=$\frac{3}{5}$.若BC=4,则AC的长度为10.
分析 根据三条平行线截两条直线,所得的对应线段成比例可得$\frac{DE}{DF}=\frac{AB}{AC}=\frac{AC-BC}{AC}$,BC=4,$\frac{DE}{DF}$=$\frac{3}{5}$,即可求出AC的长.
解答 解:∵a∥b∥c,$\frac{DE}{DF}$=$\frac{3}{5}$,BC=4,$\frac{DE}{DF}=\frac{AB}{AC}=\frac{AC-BC}{AC}$
∴$\frac{AC-4}{AC}$=$\frac{3}{5}$,
∴AC=10,
故答案为:10.
点评 本题主要考查平行线分线段成比例的知识,综合性较强,掌握三条平行线截两条直线,所得的对应线段成比例是解答此题的关键.

练习册系列答案
相关题目
16.将一长方形纸片,如图所示折叠后,再展开.若∠1=50°,则∠2=( )


| A. | 50° | B. | 60° | C. | 65° | D. | 80° |
20.下列因式分解正确的是( )
| A. | x3-x=x(x-1) | B. | x2-y2=(x-y)2 | ||
| C. | -4x2+9y2=(2x+3y)(2x-3y) | D. | x2+6x+9=(x+3)2 |
 已知,如图,C是AB的中点,AD∥CE,AD=CE.求证:△ADC≌△CEB.
已知,如图,C是AB的中点,AD∥CE,AD=CE.求证:△ADC≌△CEB.