题目内容
1.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为x1=5,x2=-1.分析 直接根据题意得出抛物线的对称轴,进而得出b的值,即可解方程得出答案.
解答 解:∵二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,
∴抛物线的对称轴为直线x=2,
则-$\frac{b}{2a}$=-$\frac{b}{2}$=2,
解得:b=-4,
∴x2+bx=5即为x2-4x-5=0,
则(x-5)(x+1)=0,
解得:x1=5,x2=-1.
故答案为:x1=5,x2=-1.
点评 此题主要考查了抛物线与x轴的交点,正确得出b的值是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知等腰三角形的一边等于4,一边等于8,那么它的周长等于( )
| A. | 16 | B. | 16或20 | C. | 20 | D. | 20或24 |

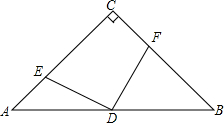 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.


