题目内容
如图，将矩形ABCD纸片沿对角线BD折叠，使点C落在C′处，C′D交AB于E，若∠BDC′=22.5°则在不添加任何辅助线的情况下，图中45°的角（图中虚线也可视为角的边）有（ ）| A、7个 | B、6个 | C、5个 | D、4个 |
考点：翻折变换（折叠问题）
专题：
分析：首先求出∠CDC′=45°，然后借助矩形的性质及三角形的内角和定理求出图中所有45°的角，问题即可解决．
解答：解：由题意得：
△BDC≌△BDC′，
∴∠C′=∠C；∠BDC=∠BDC′=22.5°，
∴∠CDC′=45°；
∵四边形ABCD为矩形，
∴∠ADC=∠A=∠C=90°，
∴∠C′=90°；
∴∠ADE=90°-45°=45°，
∴∠C′EB=∠AED=90°-45°=45°；
∴∠C′BE=90°-45°=45°；
综上所述，图中45°的角共有5个，
故选C．
解：由题意得：△BDC≌△BDC′，
∴∠C′=∠C；∠BDC=∠BDC′=22.5°，
∴∠CDC′=45°；
∵四边形ABCD为矩形，
∴∠ADC=∠A=∠C=90°，
∴∠C′=90°；
∴∠ADE=90°-45°=45°，
∴∠C′EB=∠AED=90°-45°=45°；
∴∠C′BE=90°-45°=45°；
综上所述，图中45°的角共有5个，
故选C．
点评：该命题主要考查了翻折变换及其应用问题；解题的关键是灵活运用翻折变换的特点、全等三角形的判定及其性质等几何知识，来分析、判断；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图，在方格纸中，△ABC的三个顶点和点P都在小方格的顶点上．将△ABC绕点P顺时针旋转180°，在图上画出旋转后的△A1B1C1．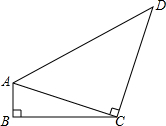
如图，四边形ABCD中，∠B=90°，AB=1，CD=8，AC⊥CD，若sin∠ACB=