题目内容
 如图,拋物线y=-
如图,拋物线y=-| 1 |
| 2 |
(1)求△ABC的面积;
(2)若P是x轴上方的抛物线上的一个动点,求点P到直线BC的距离的最大值.
考点:抛物线与x轴的交点
专题:
分析:(1)先令y=0求出AB的坐标,再令x=0求出C的坐标,根据三角形的面积公式即可得出结论;
(2)用待定系数法求出直线BC的解析式,再设出过点P且与直线垂直的直线方程,再根据此直线与抛物线有交点求出b的最大值即可.
(2)用待定系数法求出直线BC的解析式,再设出过点P且与直线垂直的直线方程,再根据此直线与抛物线有交点求出b的最大值即可.
解答:解:(1)∵令y=0,则x1=2,x2=6,
∴A(2,0),B(6,0).
∵令x=0,则y=-6,
∴C(0,-6),
∴S△ABC=
×(6-2)×6=12;
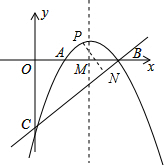 (2)设直线BC的解析式为y=kx+b(k≠0),
(2)设直线BC的解析式为y=kx+b(k≠0),
∵B(6,0),C(0,-6),
∴
,解得
,
∴直线BC的解析式为y=x-6.
设P(m,-
m2+4m-6),
在S△PCB=
×[(-
m2+4m-6)-(m-6)]×6=-
m2+9m=-
(m-3)2+
,
∴当m=3时,S最大=
,
∵BC=6
,
∴PN=
=
.
∴A(2,0),B(6,0).
∵令x=0,则y=-6,
∴C(0,-6),
∴S△ABC=
| 1 |
| 2 |
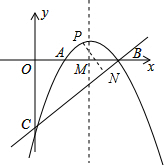 (2)设直线BC的解析式为y=kx+b(k≠0),
(2)设直线BC的解析式为y=kx+b(k≠0),∵B(6,0),C(0,-6),
∴
|
|
∴直线BC的解析式为y=x-6.
设P(m,-
| 1 |
| 2 |
在S△PCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 2 |
∴当m=3时,S最大=
| 27 |
| 2 |
∵BC=6
| 2 |
∴PN=
| 2S |
| BC |
| 9 |
| 4 |
| 2 |
点评:本题考查的是抛物线与x轴的交点问题,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
若三角形三边长之比为a:b:c=3:4:5,且a-b+c=12.则这个三角形的周长等于( )
| A、12 | B、24 | C、18 | D、36 |
 如图,A、B、C为⊙O上的三点,AB为直径,D点为弦BC的中点,OD=4,求弦AC的长度.
如图,A、B、C为⊙O上的三点,AB为直径,D点为弦BC的中点,OD=4,求弦AC的长度.