题目内容
把抛物线y=-x2+2x-1的图象向上平移m个单位,所得抛物线与x轴交点为A(x1,0),B(x2,0),且x1•x2=10.求平移后抛物线解析式.
考点:二次函数图象与几何变换
专题:
分析:根据平移后的抛物线解析式求得点A、B的坐标,然后利用根与系数的关系列出关于m的方程,通过解方程来求m的值.
解答:解:抛物线y=-x2+2x-1的图象向上平移m个单位,所得抛物线的解析式为:y=-x2+2x-1+m.
令y=0,则-x2+2x-1+m=0,
∵平移后的抛物线与x轴交点为A(x1,0),B(x2,0),且x1•x2=10,
∴x1•x2=
=10,
解得 m=-9.
则平移后的解析式为:y=-x2+2x-1-9=-x2+2x-10,即y=-x2+2x-10.
令y=0,则-x2+2x-1+m=0,
∵平移后的抛物线与x轴交点为A(x1,0),B(x2,0),且x1•x2=10,
∴x1•x2=
| -1+m |
| -1 |
解得 m=-9.
则平移后的解析式为:y=-x2+2x-1-9=-x2+2x-10,即y=-x2+2x-10.
点评:本题考查了二次函数图象与几何变换.要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目


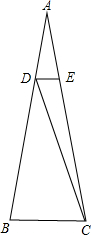 等腰△ABC中,AB=AC,∠A=20°,AD=BC,DE∥BC,求∠DCE的度数.
等腰△ABC中,AB=AC,∠A=20°,AD=BC,DE∥BC,求∠DCE的度数.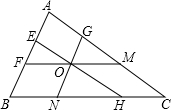 已知O是△ABC内一点,且GN∥AB,FM∥BC,EH∥AC,求证:
已知O是△ABC内一点,且GN∥AB,FM∥BC,EH∥AC,求证: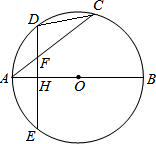 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为
 如图,拋物线y=-
如图,拋物线y=-