题目内容
观察下列关系式:
=
-
=
-
=
-
…
你可以归纳出的一般结论是
利用上述结论,计算:
+
+
+…+
.
| 1 |
| (x-1)(x-2) |
| 1 |
| x-2 |
| 1 |
| x-1 |
| 1 |
| (x-2)(x-3) |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| (x-3)(x-4) |
| 1 |
| x-4 |
| 1 |
| x-3 |
…
你可以归纳出的一般结论是
利用上述结论,计算:
| 1 |
| x-1 |
| 1 |
| (x-1)(x-2) |
| 1 |
| (x-2)(x-3) |
| 1 |
| (x-2007)(x-2008) |
考点:分式的加减法
专题:规律型
分析:先认真观察式子的特点,根据得出规律即可,根据规律展开,再合并即可.
解答:解:
=
-
(n为大于或等于1的整数),
+
+
+…+
=
+
-
+
-
+
-
+…+
-
=
,
故答案为:
=
-
(n为大于或等于1的整数).
| 1 |
| (x-n)(x-n-1) |
| 1 |
| x-n-1 |
| 1 |
| x-n |
| 1 |
| x-1 |
| 1 |
| (x-1)(x-2) |
| 1 |
| (x-2)(x-3) |
| 1 |
| (x-2007)(x-2008) |
=
| 1 |
| x-1 |
| 1 |
| x-2 |
| 1 |
| x-1 |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x-2008 |
| 1 |
| 2007 |
=
| 1 |
| 2008 |
故答案为:
| 1 |
| (x-n)(x-n-1) |
| 1 |
| x-n-1 |
| 1 |
| x-n |
点评:本题考查了分式的加减的应用,解此题的关键是能根据已知算式得出规律
=
-
(n为大于或等于1的整数).
| 1 |
| (x-n)(x-n-1) |
| 1 |
| x-n-1 |
| 1 |
| x-n |

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
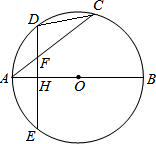 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为
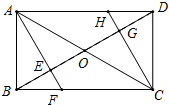 如图,矩形ABCD中,O是两条对角线的交点,AF垂直平分线段OB,垂足为E,CH垂直平分线段OD,垂足为G.求证:
如图,矩形ABCD中,O是两条对角线的交点,AF垂直平分线段OB,垂足为E,CH垂直平分线段OD,垂足为G.求证: 已知在△ABC中,∠B=∠C,BD=CE,求证:DE∥BC.
已知在△ABC中,∠B=∠C,BD=CE,求证:DE∥BC. 如图,拋物线y=-
如图,拋物线y=- 用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.
用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.