题目内容
若三角形三边长之比为a:b:c=3:4:5,且a-b+c=12.则这个三角形的周长等于( )
| A、12 | B、24 | C、18 | D、36 |
考点:解三元一次方程组
专题:
分析:设a=3k,b=4k,c=5k,代入a-b+c=12得出3k-4k+5k=12,求出k=3,即可求出三角形三边长,即可得出答案.
解答:解:设a=3k,b=4k,c=5k
代入a-b+c=12得:3k-4k+5k=12,
解得:k=3,
即a=9,b=12,c=15,
所以三角形的周长是9+12+15=36,
故选D.
代入a-b+c=12得:3k-4k+5k=12,
解得:k=3,
即a=9,b=12,c=15,
所以三角形的周长是9+12+15=36,
故选D.
点评:本题考查了解三元一次方程组的应用,解此题的关键是能得出关于k的方程.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
如果分式
中的x和y都扩大为原来的2倍,那么分式的值( )
| 2x |
| x+y |
| A、扩大2倍 | B、扩大4倍 |
| C、不变 | D、缩小2倍 |
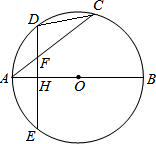 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为
 如图,拋物线y=-
如图,拋物线y=- 用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.
用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.