题目内容
17.(1)求当|x-2|+6取最小值时,x的值并求出这个最小值;(2)求当|x-2|+|x+3|取最小值时,x的取值范围并求出这个最小值;
(3)求当|x-2|+|x+3|+|x+5|取最小值时,x的值并求出这个最小值.
分析 (1)由绝对值的非负性可知当|x-2|=0式,|x-2|+6有最小知;
(2)原式可看作数轴上某点到2和-3的距离之和;
(3)原式可看作数轴上某点到2和-3和-5的距离之和.
解答 解:(1)当x=2时,原式由最小值,最小值=|2-2|+6=0+6=6;
(2)∵|x-2|+|x+3|可看作数轴上某点到2和-3的距离之和,
∴当-3≤x≤2时,|x-2|+|x+3|的最小值为2-(-3)=2+3=5;
(3)∵|x-2|+|x+3|+|x+5|可看作数轴上某点到2和-3和-5的距离之和,
∴当x=-3时,|x-2|+|x+3|+|x+5|有最小值,最小值为2-(-5)=2+5=7.
点评 本题主要考查的是绝对值的性质,利用绝对值的性质求得代数式取值最大值的条件是解题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
8.若xm-2-8yn+3是关于x,y的二元一次方程,则m+n( )
| A. | -1 | B. | 2 | C. | 1 | D. | -2 |
7. 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )
如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF交DC与点E,则图中相似三角形共有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
 如图,已知∠1、∠2(∠1>∠2),求作:∠AOB=∠1-∠2.
如图,已知∠1、∠2(∠1>∠2),求作:∠AOB=∠1-∠2.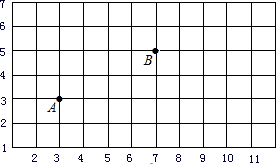 如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.
如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等. 如图,已知AA1∥BB1∥CC1,AB=2,BC=3,A1B1=1.5,求B1C1的长.
如图,已知AA1∥BB1∥CC1,AB=2,BC=3,A1B1=1.5,求B1C1的长.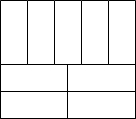 某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价110元,请计算,要完成这块绿化工程,预计花费多少元?
某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价110元,请计算,要完成这块绿化工程,预计花费多少元?