题目内容
20.先化简,再求值:($\frac{x+1}{{x}^{2}-1}$+$\frac{x}{x-1}$)÷$\frac{x+1}{{x}^{2}-2x+1}$,其中x=2tan45°.分析 先化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:($\frac{x+1}{{x}^{2}-1}$+$\frac{x}{x-1}$)÷$\frac{x+1}{{x}^{2}-2x+1}$
=$\frac{(x+1)+x(x+1)}{(x+1)(x-1)}×\frac{(x-1)^{2}}{x+1}$
=$\frac{(x+1)(x+1)}{(x+1)(x-1)}×\frac{(x-1)^{2}}{x+1}$
=x-1,
当x=2tan45°=2×1=2时,原式=x-1=2-1=1.
点评 本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
12. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)表中a的值为12;
(2)频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:请结合图表完成下列各题:
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
(2)频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
18.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
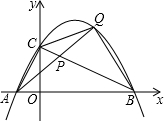 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.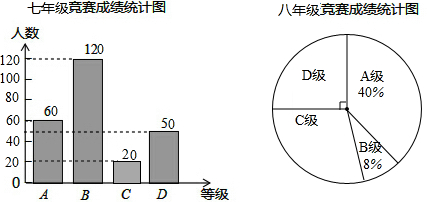
 如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.