题目内容
16. 我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.
我们规定,是函数值为零的x的值称为函数的零点,例如函数y=x-1,令y=0,可得x=1,则我们就说1是函数y=x-1的零点.(1)求一次函数y=-$\sqrt{3}$x+3$\sqrt{3}$的零点;
(2)试写出零点是-2的一个一次函数的解析式;
(3)坐标平面上有两点A(-2,0),O(0,0).试在直线y=-x+3上找一点P,使△PAO的周长最小,请求出P点的坐标及△PAO周长的最小值.
分析 (1)直接利用y=0,解方程求出答案;
(2)利用函数的零点的定义,结合一次函数的零点是-2,进而得出答案;
(3)首先得出O点关于直线y=-x+3的对称点O′,再利用轴对称的性质得出P点位置,进而得出直线AO′的解析式,求出两直线交点,再利用勾股定理得出△PAO周长的最小值.
解答 解:(1)∵y=0,
∴0=-$\sqrt{3}$x+3$\sqrt{3}$,
解得:x=3,
∴一次函数y=-$\sqrt{3}$x+3$\sqrt{3}$的零点是3;
(2)一次函数的零点是-2,则此函数可以为:y=x+2;
(3)如图所示:∵直线y=-x+3,
∴图象与x轴交点为:(3,0),与y轴交点坐标为:(0,3),
则O点关于直线y=-x+3对称点为:(3,3),
设直线AO′的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=0}\\{3k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{5}}\\{b=\frac{6}{5}}\end{array}\right.$,
故直线AO′的解析式为:y=$\frac{3}{5}$x+$\frac{6}{5}$,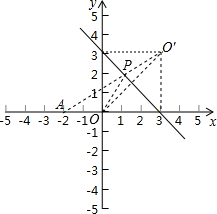
将y=-x+3与y=$\frac{3}{5}$x+$\frac{6}{5}$,联立得:
$\left\{\begin{array}{l}{y=-x+3}\\{y=\frac{3}{5}x+\frac{6}{5}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{9}{8}}\\{y=\frac{15}{8}}\end{array}\right.$,
故P($\frac{9}{8}$,$\frac{15}{8}$),
由以上可得:
∵PO=PO′,
∴△PAO周长的最小值为:AP+PO+AO=AO′+AO=2+$\sqrt{{3}^{2}+{5}^{2}}$=2+$\sqrt{34}$.
点评 此题主要考查了一次函数综合以及新定义和待定系数法求一次函数解析式以及勾股定理等知识,根据题意结合轴对称的性质得出P点位置是解题关键.

| A. | 48×106 | B. | -4.8×107 | C. | 0.48×108 | D. | 4.8×107 |
 如图,△ABC中,∠BAC=90°,D是AC上的一点,DE⊥BC于点E,且AD=DE,AE与BD相交于点F.
如图,△ABC中,∠BAC=90°,D是AC上的一点,DE⊥BC于点E,且AD=DE,AE与BD相交于点F.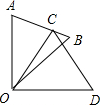 如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数.
如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数.
 已知x轴上两点A(-1,0)、B(4,0).
已知x轴上两点A(-1,0)、B(4,0).