题目内容
7.将正奇数按下表排成5列:第一列第二列第三列第四列第五列
第一行 1 3 5 7
第二行 15 13 11 9
第三行 17 19 21 23
第四行 31 29 27 25
…
根据上面规律,2007应在( )
| A. | 125行,3列 | B. | 125行,2列 | C. | 251行,2列 | D. | 251行,5列 |
分析 首先判断出2007是第1004个奇数;然后根据每行有4个奇数,用1004除以4,判断出2007在第251行;最后根据奇数行的数从小到大排列,偶数行的数从大到小排列,可得2007应在第5列,据此判断即可.
解答 解:因为(2007+1)÷2
=2008÷2
=1004
所以2007是第1004个奇数;
因为1004÷4=251,
所以2007在第251行;
又因为奇数行的数从小到大排列,偶数行的数从大到小排列,
所以2007应在第5列,
综上,可得2007应在第251行第5列.
故选:D.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:每行有4个奇数,而且奇数行的数从小到大排列,偶数行的数从大到小排列.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17.与-$\frac{1}{2}$乘积为1的数是( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | -$\frac{1}{2}$ |
 的结果是( )
的结果是( ) B.
B.  C.
C.  D. 2(x+1)
D. 2(x+1) 如图,第①个图形中一共有1个矩形,第②个图形中一共有5个矩形,第③个图形中一共有11个矩形,…则第n个图形中一共有n2+n-1矩形.
如图,第①个图形中一共有1个矩形,第②个图形中一共有5个矩形,第③个图形中一共有11个矩形,…则第n个图形中一共有n2+n-1矩形. 如图,直线a∥b,点B在直线b上,∠1=38°,∠ABC=90°,则∠2=52°.
如图,直线a∥b,点B在直线b上,∠1=38°,∠ABC=90°,则∠2=52°.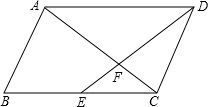 点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m.
点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m. 在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),连结AD,作∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.有下列结论:①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD=8;④3.6≤AE<10.其中正确的结论是( )
在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),连结AD,作∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.有下列结论:①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD=8;④3.6≤AE<10.其中正确的结论是( )