题目内容
16. 如图,正方形ABCD中,E是AD的中点,AB=8$\sqrt{5}$,F是线段CE上的动点,则BF的最小值是( )
如图,正方形ABCD中,E是AD的中点,AB=8$\sqrt{5}$,F是线段CE上的动点,则BF的最小值是( )| A. | 10 | B. | 12 | C. | 16 | D. | 18 |
分析 根据垂线段最短得:当BF⊥EC时,BF有最小值,利用三角形相似列比例式可得BF的长.
解答 解:当BF⊥EC时,BF有最小值,如图,
则∠BFC=90°,
∵E是AD的中点,
∴ED=$\frac{1}{2}$AD=$\frac{1}{2}$×$8\sqrt{5}$=4$\sqrt{5}$,
∵四边形ABCD是正方形,
∴∠D=90°,BC=CD=AB=8$\sqrt{5}$,
Rt△EDC中,由勾股定理得:EC=$\sqrt{(8\sqrt{5})^{2}+(4\sqrt{5})^{2}}$=20,
∵∠BFC=∠D=90°,∠FBC=∠ECD,
∴△BFC∽△CDE,
∴$\frac{BF}{CD}=\frac{BC}{CE}$,
∴$\frac{BF}{8\sqrt{5}}$=$\frac{8\sqrt{5}}{20}$,
∴BF=16,
故选C.
点评 本题考查了正方形的性质、三角形相似的性质和判定,在正方形中,常利用同角的余角证明两个角相等,为三角形全等或相似创造条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列各数:-0.101001,-3,$\sqrt{5}$,$\frac{22}{7}$,π,$\root{3}{6}$,0,$\root{3}{-1}$,其中无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.在Rt△ABC中,斜边AB上的中线CD为4cm,则斜边AB的长为( )
| A. | 2cm | B. | 12cm | C. | 8cm | D. | 16cm |
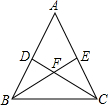 如图,等腰△ABC中,AB=AC,CD,BE是两腰上的高,说明CD=BE.
如图,等腰△ABC中,AB=AC,CD,BE是两腰上的高,说明CD=BE.




 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7. 如图,BE=AD,AB=BC,BP为一条射线,AD⊥BP,CE⊥PB,若BD=6.求EC的长.
如图,BE=AD,AB=BC,BP为一条射线,AD⊥BP,CE⊥PB,若BD=6.求EC的长.