题目内容
12.先化简,再求值:($\frac{9}{a+1}$-5+a)÷$\frac{a-2}{{a}^{2}-1}$,其中a是关于a的方程a2-3a-2=0的根.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知方程变形后代入计算即可求出值.
解答 解:原式=$\frac{9-(5-a)(a+1)}{a+1}$•$\frac{(a+1)(a-1)}{a-2}$
=$\frac{(a-2)^{2}}{a+1}$•$\frac{(a+1)(a-1)}{a-2}$
=(a-2)(a-1)
=a2-3a+2,
由a2-3a-2=0,得到a2-3a=2,
则原式=2+2=4.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.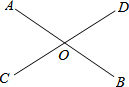 如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )
如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )
 如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )
如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )| A. | ∠A0D | B. | ∠B0D | C. | ∠B0C | D. | ∠A0B |
1.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a3)2=a6 | C. | a5÷a5=a | D. | ($\frac{y}{x}$)3=$\frac{{y}^{3}}{x}$ |
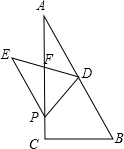 在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.