题目内容
7.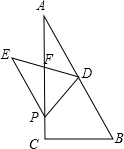 在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
在Rt△ABC中,BC=2,AC=4,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.(1)若PD⊥AB,求AP.
(2)当AD=PE时,求证:四边形BDEP为菱形.
(3)若△PDE与△ABC重合部分的面积等于△PAB面积的$\frac{1}{4}$,求AP.
分析 (1)如图1,根据勾股定理可求出AB,从而得到AD、BD的值,易证△ADP∽△ACB,只需运用相似三角形的性质就可求出AP的值;
(2)如图2,由折叠可得PE=PB,DE=DB.结合条件AD=PE,AD=DB可得PE=PB=DB=DE,即可得到四边形BDEP为菱形;
(3)根据条件可得S△PDF=$\frac{1}{4}$S△PAB=$\frac{1}{2}$S△ADP=$\frac{1}{2}$S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=$\sqrt{5}$,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=$\sqrt{5}$.
解答 解:(1)如图1,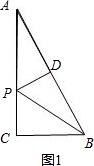
∵∠C=90°,BC=2,AC=4,
∴AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
∵点D为AB的中点,
∴AD=BD=$\sqrt{5}$.
∵PD⊥AB,
∴∠ADP=90°.
∵∠A=∠A,∠ADP=∠C,
∴△ADP∽△ACB,
∴$\frac{AP}{AB}$=$\frac{AD}{AC}$,
∴$\frac{AP}{2\sqrt{5}}$=$\frac{\sqrt{5}}{4}$,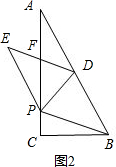
∴AP=$\frac{5}{2}$;
(2)证明:如图2,
由折叠可得:PE=PB,DE=DB.
∵AD=PE,AD=DB,
∴PE=PB=DB=DE,
∴四边形BDEP为菱形;
(3)∵点D是线段AB的中点,
∴S△ADP=S△BDP=$\frac{1}{2}$S△PAB.
由折叠可得:S△EDP=S△BDP,
∴S△PDF=$\frac{1}{4}$S△PAB=$\frac{1}{2}$S△ADP=$\frac{1}{2}$S△EDP,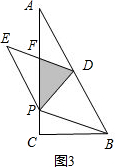
∴AF=PF,EF=DF.
①如图3,
根据三角形中位线定理可得:DF∥BP,
∴∠EDP=∠BPD.
由折叠可得∠BDP=∠EDP,
∴∠BDP=∠BPD,
∴BP=BD=$\sqrt{5}$,
∴PC=$\sqrt{P{B}^{2}-B{C}^{2}}$=$\sqrt{5-4}$=1,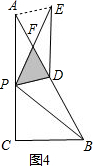
∴AP=4-1=3;
②如图4,
连接AE,
∵AF=DF,EF=PF,
∴四边形AEDP是平行四边形,
∴AP=ED,
由折叠可得:DE=DB,
∴AP=DB=$\sqrt{5}$.
综上所述:AP=3或$\sqrt{5}$.
点评 本题主要考查了相似三角形的判定与性质、平行四边形的判定与性质、菱形的判定、三角形中位线定理、勾股定理、轴对称的性质、等腰三角形的判定等知识,另外还考查了分类讨论的思想,利用S△PDF=$\frac{1}{4}$S△PAB=$\frac{1}{2}$S△ADP=$\frac{1}{2}$S△EDP得到AF=PF及EF=DF则是解决第(3)小题的关键.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | 22 | B. | 32 | C. | 62 | D. | 82 |
| 甲 | 乙 | |
| 笔记本(本) | 20 | 15 |
| 钢笔(支) | 12 | 25 |
| 总价(元) | 312 | 330 |
(2)丙购买24本笔记本和若干支钢笔共花去526元,甲发现丙的总价算错了,请通过计算加以说明.

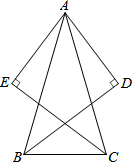 如图,△ABC为等腰三角形,AB=AC,BD分别平分∠ABC,CE分别平分∠ACB,过点A分别作BD、CE的垂线段,垂足为D、E.求证:AD=AE.
如图,△ABC为等腰三角形,AB=AC,BD分别平分∠ABC,CE分别平分∠ACB,过点A分别作BD、CE的垂线段,垂足为D、E.求证:AD=AE.