题目内容
2. 如图所示:
如图所示:(1)∠1=∠3,∠4=∠C,求证:BE平分∠ABC;
(2)BE平分∠ABC,∠4=∠C,求证:∠5=2∠3.
分析 (1)首先证明DE∥BC,进而求出∠1和∠2的关系,结论即可求出;
(2)根据角平分线的性质求出∠1=∠2,结合题干条件得到∠1=∠3,再根据三角形外角的知识得到结论.
解答 证明:(1)∵∠4=∠C,
∴DE∥BC,
∴∠3=∠2,
∵∠1=∠3,
∴∠1=∠2,
∴BE平分∠ABC;
(2)∵BE平分∠ABC,
∴∠1=∠2,
∵∠4=∠C,
∴DE∥BC,
∴∠3=∠2,
∴∠1=∠3,
∵∠5是△BDE的外角,
∴∠5=∠1+∠3=2∠3.
点评 本题主要考查了平行线的判定与性质、角平分线的性质以及三角形外角的知识,解题的关键是熟练掌握平行线的判定定理,此题难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列关于单项式-$\frac{x{y}^{3}}{2}$的说法中,正确的是( )
| A. | 系数是-$\frac{1}{2}$,次数是4 | B. | 系数是-$\frac{1}{2}$,次数是3 | ||
| C. | 系数是-2,次数是4 | D. | 系数是-2,次数是3 |
11.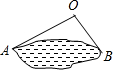 如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
 如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
如图所示,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )| A. | 5米 | B. | 15米 | C. | 10米 | D. | 20米 |
7. 如图所示,D是△ABC的边AB上的一点,∠ADC=∠BCA,AC=6,DB=5,△ABC的面积是S,则△BCD的面积是( )
如图所示,D是△ABC的边AB上的一点,∠ADC=∠BCA,AC=6,DB=5,△ABC的面积是S,则△BCD的面积是( )
 如图所示,D是△ABC的边AB上的一点,∠ADC=∠BCA,AC=6,DB=5,△ABC的面积是S,则△BCD的面积是( )
如图所示,D是△ABC的边AB上的一点,∠ADC=∠BCA,AC=6,DB=5,△ABC的面积是S,则△BCD的面积是( )| A. | $\frac{3}{5}$S | B. | $\frac{4}{7}$S | C. | $\frac{5}{9}$S | D. | $\frac{6}{11}$S |
 如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AF.连结DC、BE交于F点.
如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AF.连结DC、BE交于F点.