题目内容
9.意大利著名画家达•芬奇验证勾股定理的方法如下:(1)在一张长方形的纸板上画两个边长分别为a、b的正方形,并连接BC、FE.
(2)沿ABCDEF剪下,得两个大小相同的纸板Ⅰ、Ⅱ,请动手做一做.
(3)将纸板Ⅱ翻转后与Ⅰ拼成其他的图形.
(4)比较两个多边形ABCDEF和A′B′C′D′E′F′的面积,你能验证勾股定理吗?

分析 只要证明四边形B′C′E′F′是正方形,再证明△BOC≌△FOE,同理可证△BOC≌△B′A′F′≌△E′D′C′,推出BC=EF,B′C′=B′F′=F′E′=E′C′,设BC=EF=c,推出四边形B′C′E′F′是菱形,B′C′=c,由两个多边形ABCDEF和A′B′C′D′E′F′的面积相等,推出正方形ABOF的面积+正方形OCDE的面积=正方形B′C′F′的面积,即a2+b2=c2.
解答 解:∵四边形ABOF、四边形CDEO是正方形,
∴OB=OF,OC=OE,∠BOF=∠COE=90°,
∴∠BOC=∠FOE=90°,
在△BOC和△FOE中,
$\left\{\begin{array}{l}{OB=OF}\\{∠BOC=∠FOE=90°}\\{OC=OE}\end{array}\right.$
∴△BOC≌△FOE(SAS),
同理可证△BOC≌△B′A′F′≌△E′D′C′,
∴BC=EF,B′C′=B′F′=F′E′=E′C′,设BC=EF=c,
∴四边形B′C′E′F′是菱形,B′C′=c,
∵∠DEF=∠A′F′E′,∠OEF=∠A′F′B′,
∴∠B′F′E′=90°,
∴四边形B′C′E′F′是正方形,
∵两个多边形ABCDEF和A′B′C′D′E′F′的面积相等,
∴正方形ABOF的面积+正方形OCDE的面积=正方形B′C′F′的面积,
∴a2+b2=c2.
点评 本题考查勾股定理的证明,全等三角形的判定和性质,正方形的性质等知识,解题的关键是证明正方形ABOF的面积+正方形OCDE的面积=正方形B′C′F′的面积,体现了数形结合的思想,属于中考常考题型.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
1.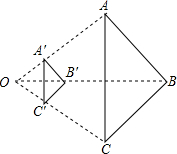 如图,以点O为位似中心,将△ABC缩小后得△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
 如图,以点O为位似中心,将△ABC缩小后得△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )| A. | 1:3 | B. | 3:1 | C. | 9:1 | D. | 1:9 |




 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.