题目内容
5. 如图为一个几何体三视图,主视图和俯视图都是矩形,则侧面积是( )
如图为一个几何体三视图,主视图和俯视图都是矩形,则侧面积是( )| A. | 8+4$\sqrt{2}$ | B. | 20+8$\sqrt{2}$ | C. | 16+8$\sqrt{2}$ | D. | 12+4$\sqrt{2}$ |
分析 应先判断出这个几何体的形状是三棱柱,进而求得侧面积.
解答 解:由主视图和俯视图可判断出这个几何体为柱体,根据左视图可得此几何体为三棱柱,侧面积由3个矩形组成,2个矩形的长与宽分别是4,2;1个矩形的长与宽分别是4,2$\sqrt{2}$,
侧面积为:
4×2×2+4×$\sqrt{2}$=16+8$\sqrt{2}$.
故选:C.
点评 考查了由三视图判断几何体,关键是得到几何体的形状,难点是判断出求几何体各个面的面积所需要的长度.

练习册系列答案
相关题目
10.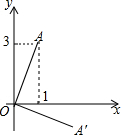 如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
 如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )
如图,已知A(1,3),将线段OA绕原点O顺时针旋转90°后得到OA′,则OA′的长度是( )| A. | $\sqrt{10}$ | B. | 3 | C. | 2$\sqrt{2}$ | D. | 1 |
17.下列几何体中,主视图相同的是( )


| A. | ①② | B. | ①④ | C. | ①③ | D. | ②④ |
15.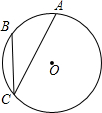 如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )
如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )
 如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )
如图,点A、B、C在半径为9的⊙O上,∠ACB=30°.则$\widehat{AB}$的长是( )| A. | π | B. | $\frac{3π}{2}$ | C. | 2π | D. | 3π |
 如图,若正三棱柱看不见的一个侧面与投影面平行,则这个正三棱柱的正投影是( )
如图,若正三棱柱看不见的一个侧面与投影面平行,则这个正三棱柱的正投影是( )