题目内容
8.用描点法作出函数y=$\left\{\begin{array}{l}{2x(0≤x≤3)}\\{3x-3(x>3)}\end{array}\right.$的图象,并求当y=36时,x的值.分析 列出相应的表格,如图所示,根据表格得函数图象上的点,在已知平面直角坐标系中描出各点,然后作出一次函数图象,如图所示;把y=36代入y=3x-3,求得即可.
解答 解:作出表格如图所示,
| x | 0 | 1 | 3 | 4 |
| y=2x | 0 | 2 | ||
| y=3x-3 | 6 | 9 |

把y=36代入y=3x-3得,36=3x-3,解得x=13.
点评 此题考查了一次函数的图象以函数图象上点的坐标特征,其中作函数图象的步骤为:列表;描点;连线.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
18.计算$\frac{1}{a-1}-\frac{a}{a-1}$的结果是( )
| A. | -1 | B. | 1 | C. | $\frac{1+a}{a-1}$ | D. | 2 |
20.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里,客轮以60海里/小时的速度沿北偏西60°方向航行$\frac{2}{3}$小时到达B处,那么tan∠BAP=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
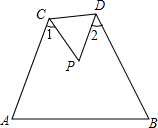 如图,△ABP沿CD折叠,求证:∠1+∠2=2∠P.
如图,△ABP沿CD折叠,求证:∠1+∠2=2∠P.