题目内容
17.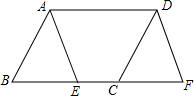 如图,在四边形ABCD中,AB=CD,AB∥CD,点E在边BC上,点F在BC的延长线上,且BE=CF,求证:△ABE≌△DCF.
如图,在四边形ABCD中,AB=CD,AB∥CD,点E在边BC上,点F在BC的延长线上,且BE=CF,求证:△ABE≌△DCF.
分析 先利用平行线的性质得到∠B=∠DCF,然后根据“SAS”可判断△ABE≌△DCF.
解答 证明:∵AB∥CD,
∴∠B=∠DCF,
在△ABE和△DCF中
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠DCF}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△DCF(SAS).
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
相关题目
6.数学应用:在“课内比教学”活动中,16位评委给吴老师的讲课比赛平分都在90分左右,把吴老师的得分超过或不足90分的部分分别用正、负数表示(单位:分),统计如下表:
(1)吴老师一共得了多少分?
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
| 超过或不足90分的部分 | -5 | -2.5 | -1 | 0 | 0.5 | 2 | 3 | 6 |
| 评委人数 | 2 | 2 | 3 | 4 | 2 | 1 | 1 | 1 |
(2)比赛选手得分计算方法:先去掉一个最高分,去掉一个最低分,然后计算出平均分,按此计算,吴老师的讲课比赛得分是多少?
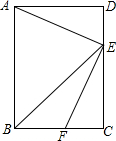 如图,在矩形中,BE平分∠ABC,交CD于点E,点F在边BC上.
如图,在矩形中,BE平分∠ABC,交CD于点E,点F在边BC上.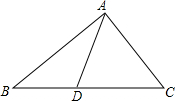 如图,点D是△ABC的边BC上任意一点,则AB+BC+AC>2AD.请说明理由.
如图,点D是△ABC的边BC上任意一点,则AB+BC+AC>2AD.请说明理由. 如图,斜坡AB的坡度为1:5,该段斜坡的长度为60m,求坡顶B点的垂直高度.
如图,斜坡AB的坡度为1:5,该段斜坡的长度为60m,求坡顶B点的垂直高度.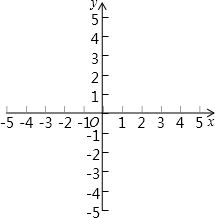 如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象
如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象