题目内容
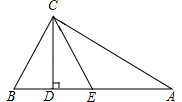如图，△ABC中，∠ACB=90°，AC＞BC，CD、CE分别为斜边AB上的高和中线，若tan∠DCE=| 2 |
| 3 |
| BC |
| AC |
考点：解直角三角形
专题：
分析：首先利用直角三角形的性质得出CE=BE，进而利用勾股定理表示出BE以及BD的长，再利用锐角三角函数关系得出即可．
解答：解：∵∠ACB=90°，CE为斜边AB上的中线，
∴CE=AE=BE，∠B+∠A=90°，
∵CD⊥AB，
∴∠B+∠BCD=90°，
∴∠BCD=∠A，
∵tan∠DCE=
，
设DE=2x，则DC=3x，
∴CE=
x，故BE=
x，
∴BD=
x-2x，
∴tanA=tan∠BCD=
=
=
．
故答案为：
．
∴CE=AE=BE，∠B+∠A=90°，
∵CD⊥AB，
∴∠B+∠BCD=90°，
∴∠BCD=∠A，
∵tan∠DCE=
| 2 |
| 3 |
设DE=2x，则DC=3x，
∴CE=
| 13 |
| 13 |
∴BD=
| 13 |
∴tanA=tan∠BCD=
| BD |
| CD |
| ||
| 3x |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：此题主要考查了解直角三角形，熟练掌握锐角三角函数关系是解题关键．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
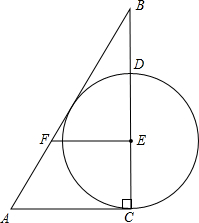已知：如图，Rt△ABC，∠ACB=90°，点E是边BC上一点，过点E作FE⊥BC（垂足为E）交AB于点F，且EF=AF，以点E为圆心，EC长为半径作⊙E交BC于点D