题目内容
用同一种规格的正多边形地砖铺满地面,这种地砖的形状可能是 .(写出一种即可)
考点:平面镶嵌(密铺)
专题:开放型
分析:利用正三角形的每个内角是60°,能整除360度.正方形的每个内角是90°,4个能密铺.正六边形的每个内角是120°,能整除360°,能密铺,即可得出答案.
解答:解:用同一种正多边形地砖镶嵌成平整的地面,那么这种正多边形地砖的形状可以是
如:正三角形(答案不唯一);
故答案为:正三角形(答案不唯一).
如:正三角形(答案不唯一);
故答案为:正三角形(答案不唯一).
点评:本题考查的知识点是:一种正多边形的镶嵌应符合一个内角度数能整除360°.

练习册系列答案
相关题目
把三角形三边的长度都扩大为原来的2倍,则锐角A的正弦函数值( )
| A、扩大为原来的2倍 | ||
B、缩小为原来的
| ||
| C、不变 | ||
| D、不能确定 |
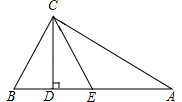 如图,△ABC中,∠ACB=90°,AC>BC,CD、CE分别为斜边AB上的高和中线,若tan∠DCE=
如图,△ABC中,∠ACB=90°,AC>BC,CD、CE分别为斜边AB上的高和中线,若tan∠DCE=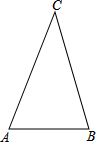 如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成的△PAB,△PBC,△PAC均为等腰三角形,则满足上述条件的所有点P有
如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成的△PAB,△PBC,△PAC均为等腰三角形,则满足上述条件的所有点P有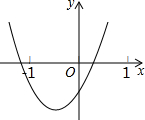 二次函数y=ax2+bx+c的图象如图所示,则a
二次函数y=ax2+bx+c的图象如图所示,则a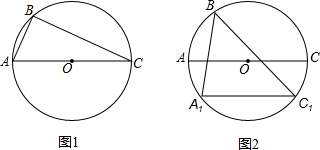 如图在⊙O中,图1中△ABC内接于⊙O且∠ABC=90°,图2中△A1BC1,内接于⊙O,AC是直径且AC∥A1C1,请仅用无刻度的直尺按要求画图.
如图在⊙O中,图1中△ABC内接于⊙O且∠ABC=90°,图2中△A1BC1,内接于⊙O,AC是直径且AC∥A1C1,请仅用无刻度的直尺按要求画图. 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠AOB的度数为
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠AOB的度数为