题目内容
在△ABC,D为BC中点,AD=AC,DE⊥BC,与AB交于E,EC与AD交于F,求证:AF=FD.
考点:平行四边形的判定与性质
专题:证明题
分析:作AG⊥CD,交CD于G,交CE于H,连接DH,根据等腰三角形的性质求得AG垂直平分CD,进而求得CH=DH,∠BCE=∠CDH.根据垂直平分线的性质求得CE=BE,
根据等边对等角得出∠BCE=∠B,从而证得∠B=∠CDH.得出AB∥DH.进一步求得AG∥DE,根据平行四边形的概念得出四边形AHDE是平行四边形,根据平行四边形的性质得出AF=DF.
根据等边对等角得出∠BCE=∠B,从而证得∠B=∠CDH.得出AB∥DH.进一步求得AG∥DE,根据平行四边形的概念得出四边形AHDE是平行四边形,根据平行四边形的性质得出AF=DF.
解答: 证明:如图,作AG⊥CD,交CD于G,交CE于H,连接DH,
证明:如图,作AG⊥CD,交CD于G,交CE于H,连接DH,
∵AC=AD,
∴△ACD是等腰三角形.
又∵AG⊥CD,
∴AG垂直平分CD,
∴CH=DH,
∴∠BCE=∠CDH.
∵D为BC的中点,DE垂直平分BC,
∴CE=BE,
∴∠BCE=∠B,
∴∠B=∠CDH.
∴AB∥DH.
∵AG⊥BC,DE⊥BC,
∴AG∥DE,
∵AB∥DH,AG∥DE,
∴四边形AHDE是平行四边形,
∴AF=DF.
 证明:如图,作AG⊥CD,交CD于G,交CE于H,连接DH,
证明:如图,作AG⊥CD,交CD于G,交CE于H,连接DH,∵AC=AD,
∴△ACD是等腰三角形.
又∵AG⊥CD,
∴AG垂直平分CD,
∴CH=DH,
∴∠BCE=∠CDH.
∵D为BC的中点,DE垂直平分BC,
∴CE=BE,
∴∠BCE=∠B,
∴∠B=∠CDH.
∴AB∥DH.
∵AG⊥BC,DE⊥BC,
∴AG∥DE,
∵AB∥DH,AG∥DE,
∴四边形AHDE是平行四边形,
∴AF=DF.
点评:本题考查了等腰三角形的判定和性质,线段的垂直平分线的性质,平行四边形的判定和性质等,熟练掌握性质定理是关键.

练习册系列答案
相关题目
 如图,BC、AC相交于点E,AB∥EF∥CD,若AB=6,CD=9,求EF的长.
如图,BC、AC相交于点E,AB∥EF∥CD,若AB=6,CD=9,求EF的长.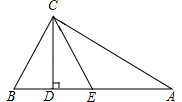 如图,△ABC中,∠ACB=90°,AC>BC,CD、CE分别为斜边AB上的高和中线,若tan∠DCE=
如图,△ABC中,∠ACB=90°,AC>BC,CD、CE分别为斜边AB上的高和中线,若tan∠DCE=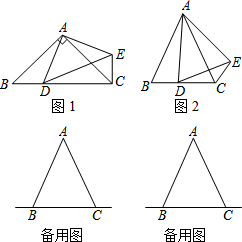 在△ABC中,AB=AC,点D是线段BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
在△ABC中,AB=AC,点D是线段BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.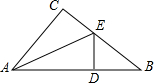 在△ABC中,∠C=90°,AC=6,BC=8,AE平分∠CAE,ED⊥AB,求BE的长.
在△ABC中,∠C=90°,AC=6,BC=8,AE平分∠CAE,ED⊥AB,求BE的长.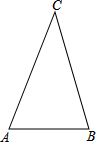 如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成的△PAB,△PBC,△PAC均为等腰三角形,则满足上述条件的所有点P有
如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成的△PAB,△PBC,△PAC均为等腰三角形,则满足上述条件的所有点P有 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠AOB的度数为
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠AOB的度数为