题目内容
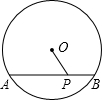如图，AB是⊙O的弦，P是线段AB上一动点，OP长度满足2≤OP≤3，则AB=考点：垂径定理,勾股定理
专题：
分析：过点O作OD⊥AB于点D，连接OA，则AB=2AD，根据OP长度满足2≤OP≤3可知当P与D重合时最短，与A重合时最长，故OD=2，OA=3，再由勾股定理求出AD的长，进而可得出结论．
解答：
解：过点O作OD⊥AB于点D，连接OA，则AB=2AD，
∵OP长度满足2≤OP≤3，
∴当P与D重合时最短，与A重合时最长，
∴OD=2，OA=3，
∴AD=
=
=
，
∴AB=2
．
故答案为：2
．
解：过点O作OD⊥AB于点D，连接OA，则AB=2AD，∵OP长度满足2≤OP≤3，
∴当P与D重合时最短，与A重合时最长，
∴OD=2，OA=3，
∴AD=
| OA2-OD2 |
| 32-22 |
| 5 |
∴AB=2
| 5 |
故答案为：2
| 5 |
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知S1=1，S2=3，S3=2，S4=4，求S5、S6、S7的值．
如图所示，在Rt△ABC中，∠C=90°，∠B=45°，D是BC上一点，∠ADC=60°，BD=10，求CD和AC的长．（结果保留根号）
如图：⊙O1和⊙O2是等圆，P是O1O2的中点．过点P作直线AD交⊙O1于点A、B，交⊙O2于点C、D，求证：AB=CD．
如图，平行四边形ABCD的面积为36，对角线AC，BD交于点O点，E为CD上一点，已知四边形EFOG的面积为3，则阴影部分的面积为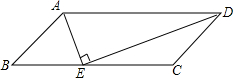
如图，?ABCD中，AE平分∠BAD，交BC于E，DE⊥AE，下列结论：①DE平分∠ADC；②E是BC的中点；③AD=2CD；④梯形ADCE的面积与△ABE的面积比是3：1，其中正确的个数是（ ）
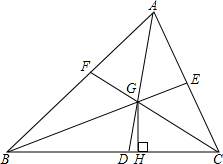如图，在△ABC中，AD，BE，CF是角平分线，交点是点G，GH⊥BC，试说明∠BGD=∠CGH的理由．
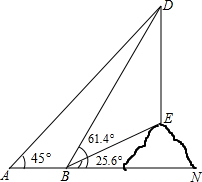如图，课外数学活动小组要测量小山坡上塔的高度DE，DE所在直线与水平线AN垂直，他们在A处测塔尖D的仰角为45°，再沿着射线AN方向前进50米到达B处，此时测得塔尖D的仰角∠DBN=61.4°，塔底E的仰角∠EBN=25.6°，现在请你帮助课外活动小组算一算塔高DE大约是多少米？（结果精确到个位）（参考数据：sin25.6°≈0.4，cos25.6°≈0.9，tan25.6°≈0.5，sin61.4°≈0.9，cos61.4°≈0.5，tan61.4°≈1.8）
如图所示，已知点E在AB上，且CE平分∠BCD，DE平分∠ADC，∠EDC+∠DCE=90°，试说明AD∥BC．