题目内容
 如图所示,在Rt△ABC中,∠C=90°,∠B=45°,D是BC上一点,∠ADC=60°,BD=10,求CD和AC的长.(结果保留根号)
如图所示,在Rt△ABC中,∠C=90°,∠B=45°,D是BC上一点,∠ADC=60°,BD=10,求CD和AC的长.(结果保留根号)考点:勾股定理,含30度角的直角三角形,等腰直角三角形
专题:
分析:首先在Rt△ACD中,利用直角三角形的性质求得CD的长,再进一步根据勾股定理求得AC的长.
解答:解:在Rt△ACD中,设CD=x,
∵∠C=90°,∠ADC=60°,tan60°=
=
,
∴AC=
x,
在Rt△ACB中,∠C=90°,∠ABC=45°,
∴AC=BC,BD=10,
∴
x=x+10,
解得:x=
=5(
+1)=5
+5,
∴AC=
x=15+5
,即AC=BC=15+5
,
∴CD=BC-BD=15+5
-10=5+5
.
∵∠C=90°,∠ADC=60°,tan60°=
| AC |
| CD |
| 3 |
∴AC=
| 3 |
在Rt△ACB中,∠C=90°,∠ABC=45°,
∴AC=BC,BD=10,
∴
| 3 |
解得:x=
| 10 | ||
|
| 3 |
| 3 |
∴AC=
| 3 |
| 3 |
| 3 |
∴CD=BC-BD=15+5
| 3 |
| 3 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知BD、CE是△ABC的中线,M、N分别是BD、CE的中点,那么MN:BC=
已知BD、CE是△ABC的中线,M、N分别是BD、CE的中点,那么MN:BC= 已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,
已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50, 如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.
如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由. 如图,在平面直角坐标系中,点A的坐标为(2,1).
如图,在平面直角坐标系中,点A的坐标为(2,1).
 如图,北部湾海面有一艘某军的军舰正在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东60°方向.且在B的北偏西30°方向,军舰从B处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时)(
如图,北部湾海面有一艘某军的军舰正在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东60°方向.且在B的北偏西30°方向,军舰从B处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时)(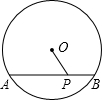 如图,AB是⊙O的弦,P是线段AB上一动点,OP长度满足2≤OP≤3,则AB=
如图,AB是⊙O的弦,P是线段AB上一动点,OP长度满足2≤OP≤3,则AB= 如图,若∠2=∠6,则
如图,若∠2=∠6,则