题目内容
15．
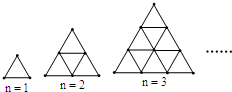如图，是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，当每边摆上20（n=20）根时，需火柴棍为630 根，若当每边摆上n根时，试写出需火柴棍为$\frac{3n（1+n）}{2}$ 根．
分析 根据图中规律可发现，每边增加一根火柴，火柴总数就会比前面增加3n根火柴．
解答 解：由图形可知：当n=1时，火柴总数为3×1，
当n=2时，火柴总数为3×（1+2），
当n=3时，火柴总数为3×（1+2+3），
∴当n=20时，火柴总数为3×（1+2+3+…+20）=630，
当每边摆上n根式，火柴总数为3×（1+2+3+…+n）=$\frac{3n（1+n）}{2}$，
点评 本题考查数字规律，要注意每一个图形之间的联系是解本题的关键．
练习册系列答案
相关题目
如图，CD是⊙O的直径，点E在⊙O上，A为DC延长线上一点，连接AE交⊙O于点B，且⊙O得半径为2，若∠EOD=3∠A，求AB的长．
如图所示，∠B=∠D，∠A=∠C，求证：∠1=∠2．
7．
如图：∠1=（ ）度．
如图：∠1=（ ）度．| A． | 60 | B． | 80 | C． | 100 | D． | 140 |
如图，在等腰直角△ABC中，点P为斜边AB上一动点（不与A、B两点重合），以CP为斜边在直线CP左侧作等腰直角△CPD．