题目内容
8.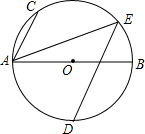 如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.
如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.
分析 连接AD、BD、BE,先证得△ADB是等腰直角三角形,进而证得∠E=45°,根据AC∥DE,得出∠CAE=45°,然后根据tan(45°+∠EAB)=$\frac{tan45°+tan∠EAB}{1-tan45°•tan∠EAB}$=$\frac{1+tan∠EAB}{1-tan∠EAB}$=2,求得tan∠EAB=$\frac{1}{3}$,根据勾股定理即可求得AE的长.
解答  解:连接AD、BD、BE,
解:连接AD、BD、BE,
∵$\widehat{AD}=\widehat{BD}$,
∴AD=BD,
∵AB是直径,
∴∠ADB=90°,∠AEB=90°,
∴∠ABD=∠BAD=45°,
∴∠E=∠ABD=45°,
∵AC∥DE,
∴∠CAE=∠E=45°,
∴∠CAB=∠CAE+∠EAB=45°+∠EAB,
∴tan∠CAB=tan(45°+∠EAB)=2,
∵tan(45°+∠EAB)=$\frac{tan45°+tan∠EAB}{1-tan45°•tan∠EAB}$=$\frac{1+tan∠EAB}{1-tan∠EAB}$=2,
∴tan∠EAB=$\frac{1}{3}$,
在RT△ABE中,tan∠EAB=$\frac{BE}{AE}$=$\frac{1}{3}$,
∴AE=3BE,
∵AE2+BE2=AB2,
即AE2+($\frac{1}{3}$AE)2=AB2,
∵AB=4$\sqrt{5}$,
∴AE=6$\sqrt{2}$.
故答案为:6$\sqrt{2}$.
点评 本题考查了圆周角定理,平行线的性质,勾股定理以及直角三角函数等,求得tan∠EAB=$\frac{1}{3}$是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
13. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )
如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )
 如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )
如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )| A. | (-3,1) | B. | (-2,-1) | C. | (-1,1) | D. | (1,-2) |
 已知:如图,E,F是?ABCD的对角线AC上的点,∠ABE=∠CDF.求证:AE=CF.
已知:如图,E,F是?ABCD的对角线AC上的点,∠ABE=∠CDF.求证:AE=CF. 如图,△ABC中,∠ACB的平分线交AB于D,DE⊥BC,垂足是E,DF∥BC,交AC于F,∠1=35°,∠2=∠B,求∠A.
如图,△ABC中,∠ACB的平分线交AB于D,DE⊥BC,垂足是E,DF∥BC,交AC于F,∠1=35°,∠2=∠B,求∠A.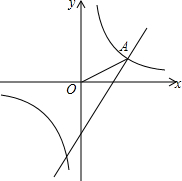 如图,在同一直角坐标系中,一次函数y=$\sqrt{3}$x-2的图象和反比例函数y=$\frac{k}{x}$的图象的一个交点为A($\sqrt{3}$,m).
如图,在同一直角坐标系中,一次函数y=$\sqrt{3}$x-2的图象和反比例函数y=$\frac{k}{x}$的图象的一个交点为A($\sqrt{3}$,m).