题目内容
18. 已知:如图,E,F是?ABCD的对角线AC上的点,∠ABE=∠CDF.求证:AE=CF.
已知:如图,E,F是?ABCD的对角线AC上的点,∠ABE=∠CDF.求证:AE=CF.
分析 由四边行ABCD是平行四边形,可得AB=CD,AB∥CD,即可证得∠BAE=∠DCF,又由∠ABE=∠CDF,则可证得△ABE≌△CDF,继而证得结论.
解答 证明:∵四边行ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠BAE=∠DCF}\\{AB=CD}\\{∠ABE=∠CDF}\end{array}\right.$,
∴△ABE≌△CDF(ASA),
∴AE=CF.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意平行四边形的对边平行且相等是解题关键.

练习册系列答案
相关题目
8.下列图形中不可能是正多边形的是( )
| A. | 三角形 | B. | 正方形 | C. | 四边形 | D. | 梯形 |
3.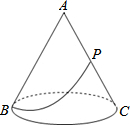 如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
 如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )| A. | 5m | B. | $3\sqrt{5}$m | C. | 6m | D. | $2\sqrt{5}$m |
10.2010年前三季度,我市接待旅游者365000人次,那么3665000用科学记数法表示为( )
| A. | 36.65×105 | B. | 3.665×106 | C. | 3.665×107 | D. | 0.3665×105 |
 如图,用一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=-8.
如图,用一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=-8.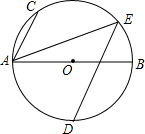 如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.
如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.