题目内容
18.计算题:(1)$\sqrt{12}+\sqrt{48}-\sqrt{75}$
(2)$\frac{{\sqrt{72}-\sqrt{16}}}{{\sqrt{8}}}-{({\sqrt{2}-1})^2}$
(3)$2sin30°+\sqrt{3}tan60°+2{cos^2}45°$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的除法和乘法运算,然后合并即可;
(3)根据特殊角的三角函数值得到原式=2×$\frac{1}{2}$+$\sqrt{3}$×$\sqrt{3}$+2×($\frac{\sqrt{2}}{2}$)2,然后进行二次根式的乘法运算后合并即可.
解答 解:(1)原式=2$\sqrt{3}$+4$\sqrt{3}$-5$\sqrt{3}$
=$\sqrt{3}$;
(2)原式=$\sqrt{\frac{72}{8}}$-$\sqrt{\frac{16}{8}}$-(2-2$\sqrt{2}$+1)
=3-$\sqrt{2}$-3+2$\sqrt{2}$
=$\sqrt{2}$;
(3)原式=2×$\frac{1}{2}$+$\sqrt{3}$×$\sqrt{3}$+2×($\frac{\sqrt{2}}{2}$)2
=1+3+1
=5.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
6.某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.
(1)试求y与x之间的函数表达式.
(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式.
(毛利润=销售总价-成本总价)
| X(元/件) | 35 | 40 | 45 | 50 | 55 |
| Y(件) | 550 | 500 | 450 | 400 | 350 |
(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式.
(毛利润=销售总价-成本总价)
10.四张背面完全一样圆形纸片,正面图案如下,将这四张纸片背面朝上摞在一起洗,匀后从中随机抽取2张,其中有中心对称图形的概率是( )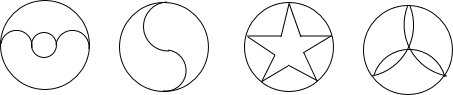

| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
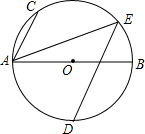 如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.
如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$. 如图,胶州湾大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是三角形的稳定性.
如图,胶州湾大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是三角形的稳定性.
 如图所示,一个不等式组的解集表示在数轴上,这个不等式组可能是$\left\{\begin{array}{l}{x≤3}\\{x>-1}\end{array}\right.$.
如图所示,一个不等式组的解集表示在数轴上,这个不等式组可能是$\left\{\begin{array}{l}{x≤3}\\{x>-1}\end{array}\right.$.