题目内容
20.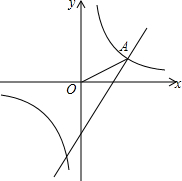 如图,在同一直角坐标系中,一次函数y=$\sqrt{3}$x-2的图象和反比例函数y=$\frac{k}{x}$的图象的一个交点为A($\sqrt{3}$,m).
如图,在同一直角坐标系中,一次函数y=$\sqrt{3}$x-2的图象和反比例函数y=$\frac{k}{x}$的图象的一个交点为A($\sqrt{3}$,m).(1)求m的值及反比例函数的解析式.
(2)若点P在x轴上,且△AOP为等腰三角形,请直接写出点P的坐标.
分析 (1)把A($\sqrt{3}$,m)代入一次函数的解析式,即可求得n的值,即A的坐标,然后把A的坐标代入反比例函数的解析式,即可求得函数的解析式;
(2)分三种情况进行讨论:OA=OP时两个点(2,0),(-2,0),PA=PO时一个点($\frac{{2\sqrt{3}}}{3}$,0),AO=AP时一个点(2$\sqrt{3}$,0),求得P的坐标.
解答 解:(1)∵一次函数$y=\sqrt{3}x-2$的图象经过点A($\sqrt{3}$,m),
∴$m=\sqrt{3}×\sqrt{3}-2=1$,
∴点A的坐标为($\sqrt{3}$,1),
又∵反比例函数$y=\frac{k}{x}$的图象经过点A,
∴$k=\sqrt{3}×1=\sqrt{3}$,
∴反比例函数的解析式为$y=\frac{{\sqrt{3}}}{x}$;
(2)符合条件的点P有4个,分别是:P1(-2,0),P2(2,0),P3($2\sqrt{3}$,0),P4($\frac{{2\sqrt{3}}}{3}$,0).
点评 本题是反比例函数与一次函数的交点问题,等腰三角形知识,要注意(2)在不确定等腰三角形的腰和底的情况下要考虑到所有的情况,不要漏解.

练习册系列答案
相关题目
10.2010年前三季度,我市接待旅游者365000人次,那么3665000用科学记数法表示为( )
| A. | 36.65×105 | B. | 3.665×106 | C. | 3.665×107 | D. | 0.3665×105 |
12.下列命题中是假命题的是( )
| A. | 如果一个直角三角形的两条直角边与另一个直角三角形的两条直角边对应相等,那么这两个直角三角形全等 | |
| B. | 等腰三角形顶角的平分线把它分成两个全等的三角形 | |
| C. | 周长相等的两个三角形全等 | |
| D. | 有一条直角边对应相等的两个等腰直角三角形全等 |
10.四张背面完全一样圆形纸片,正面图案如下,将这四张纸片背面朝上摞在一起洗,匀后从中随机抽取2张,其中有中心对称图形的概率是( )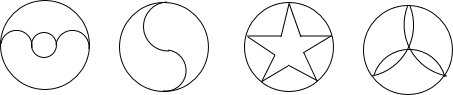

| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
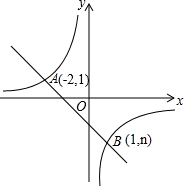 已知:如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,
已知:如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,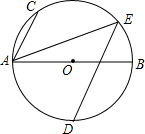 如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.
如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.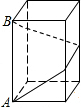 如图,长方体的底面是边长为1的正方形,长方体的高为3,如果用一根无弹力的细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短的是( )
如图,长方体的底面是边长为1的正方形,长方体的高为3,如果用一根无弹力的细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短的是( )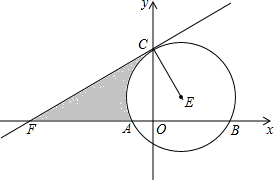 如图,半径为2的⊙E交x轴于A、B,交y轴于点C、D,直线CF交x轴负半轴于点F,连接EC.已知点E的坐标为(1,1),∠OFC=30°.
如图,半径为2的⊙E交x轴于A、B,交y轴于点C、D,直线CF交x轴负半轴于点F,连接EC.已知点E的坐标为(1,1),∠OFC=30°.