题目内容
19.一个三角形的三边分别为2a,$\sqrt{2}a$,$\sqrt{2}a$,则它的三个内角的度数分别为45°,45°,90°.分析 根据勾股定理的逆定理可知这个三角形是直角三角形,然后根据等腰三角形的判定得到这个三角形是等腰直角三角形.
解答 解:∵三角形的三边分别为2a,$\sqrt{2}a$,$\sqrt{2}a$,
∴($\sqrt{2}$a)2+($\sqrt{2}$a)2=4a2=(2a)2,
∴这个三角形是直角三角形,
∵$\sqrt{2}a$=$\sqrt{2}a$,
∴这个三角形是等腰直角三角形,
∴三个内角的度数分别为:45°,45°,90°.
故答案为:45°,45°,90°.
点评 本题考查了勾股定理的逆定理的运用,熟记勾股定理的逆定理是解题的关键.

练习册系列答案
相关题目
10.2010年前三季度,我市接待旅游者365000人次,那么3665000用科学记数法表示为( )
| A. | 36.65×105 | B. | 3.665×106 | C. | 3.665×107 | D. | 0.3665×105 |
 如图所示,直线l1∥l2,AB⊥D于点E,如果∠1=34°,求∠2的度数.
如图所示,直线l1∥l2,AB⊥D于点E,如果∠1=34°,求∠2的度数.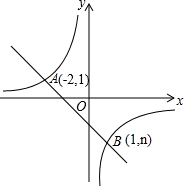 已知:如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,
已知:如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,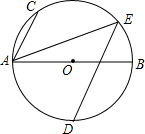 如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.
如图,AB为⊙O的直径,点C,D,E为⊙O上的点,AC∥DE,AB=4$\sqrt{5}$,tan∠CAB=2,$\widehat{AD}=\widehat{BD}$,则AE的长为6$\sqrt{2}$.